In the recent article about the Cryptarchia consensus protocol, we introduced nullifiers as a way to represent spent data units, known as notes, in a Nomos native zone. In this model, a zone’s ledger includes a set of nullifiers that keeps track of all the notes spent in that zone. To spend a note, a proof that the note’s nullifier is not present in the zone’s nullifier set must be produced. Therefore, the structure of the nullifier set was required to be fairly compact to facilitate storage of an ever-growing set of nullifiers, while also facilitating efficient non-membership proof generation.

The Nomos Team narrowed down the choices for the structure of the nullifier set to two types of Merkle trees: Sparse Merkle Trees (SMTs) and Indexed Merkle Trees (IMTs). This article will introduce these Merkle tree structures from the perspective of nullifier sets for Nomos zones, and will describe the relative advantages of each. In the end, we will also explain the decision of the Nomos Team to use IMTs to implement these sets.

The Nomos Zone Ledger Model and the ‘Ideal’ Nullifier Set

Nomos uses notes to represent transferrable and ownable data, with these data being private by default. Notes are bound to their owners and are associated with the particular zone where they are held. Despite this, notes have a common framework to enable them to be transferred between Nomos zones, the autonomous network state rollups that form the client-facing part of the Nomos Network. Note transfer transactions are based on the UTXO model where a sender spends their note and creates an equivalent new note belonging to the recipient. A spent note can never be spent again.

In this model, a representation called a nullifier is created for every spent note, calculated as the hash of the note’s secret key appended to its commitment to ensure privacy. This privacy emerges due to the unlinkability between commitments and nullifiers created by the hash function. Nullifiers for all notes spent in a zone are stored in that zone’s nullifier set, and therefore a note nullifier’s absence in a zone’s nullifier set means that the note has not yet been spent. It is therefore necessary to prove that a note’s nullifier is not a member of the nullifier set in order to be able to spend a note.

Because new nullifiers are added to a zone’s nullifier set whenever notes are spent and are never removed, a nullifier set must be able to handle a very large number of nullifiers. Based on a figure of about $2^{27}$ nullifiers produced by Zcash since its launch in 2016, the Nomos team chose an upper limit of $2^{64}$ nullifiers per set, which would last for a very long time at Zcash’s nullifier production rate.

As a result, nullifier sets should be scalable to be able to handle large amounts of nullifiers. Since proofs of non-membership can be computationally complex, the nullifier set structure should be especially performant in its handling of these operations. This performance is also reflected in the complexity of the ZK circuit used to verify non-membership proofs. It was also deemed important to have a design that is easy to implement, without excessive complexity that may lead to errors. With these evaluation criteria in mind, we can proceed to analyse the possibilities for the nullifier set structure for Nomos zones.

Sparse Merkle Trees

A Sparse Merkle Tree (SMT) is a type of Merkle tree designed to store data in a way that allows for efficient verification of data existence or non-existence. Like other binary Merkle trees, it consists of elements known as leaf nodes, adjacent pairs of which are concatenated and hashed to produce internal nodes. These nodes are in turn concatenated and hashed again, repeating the process until a single root node is reached. SMTs are characterised by their large, fixed size - with leaves representing every possible element of the set such that the leaf’s index corresponds to the stored value. If an element is present in the SMT, the corresponding leaf is set to $1$. All other leaves are initialised to default $0$ values.

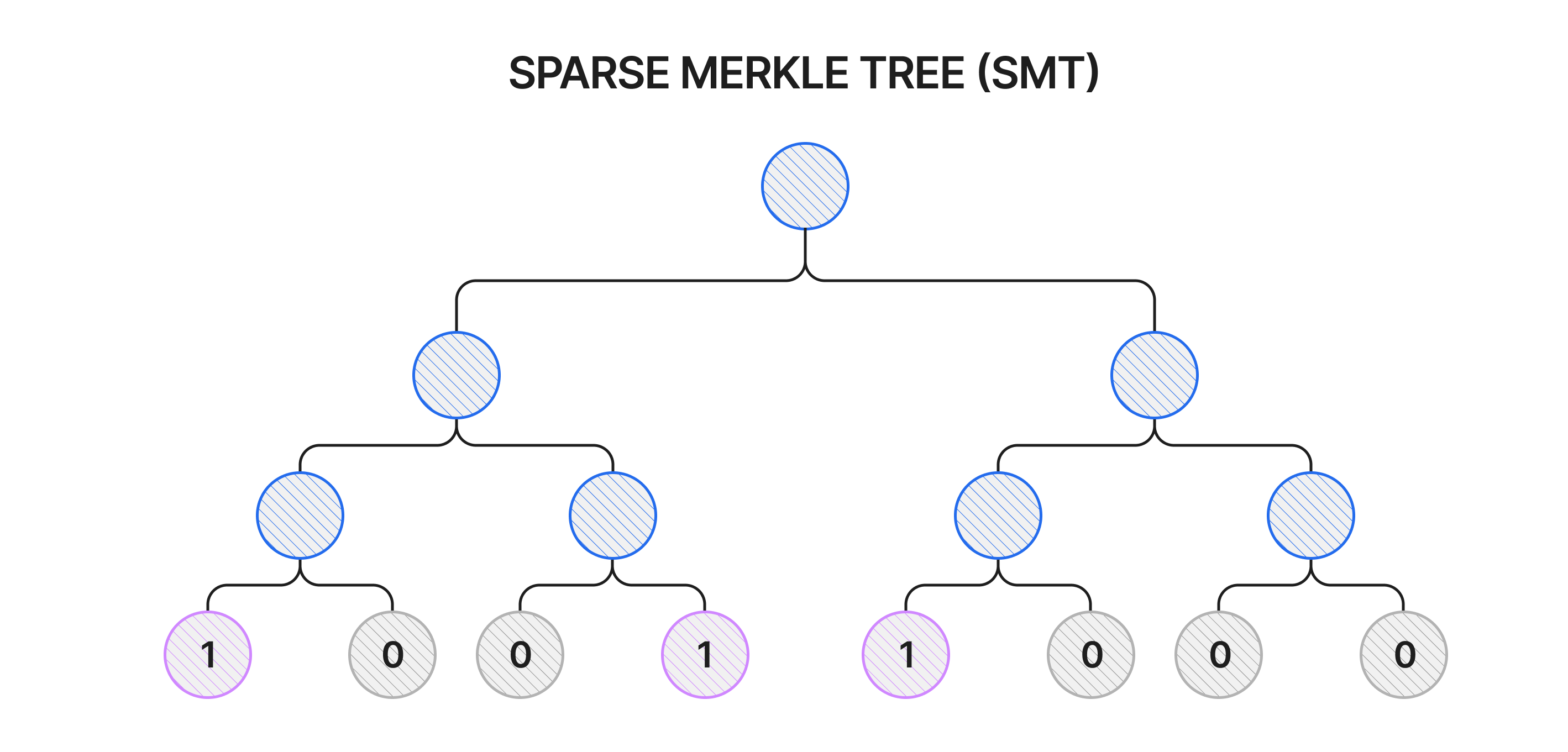
For example, to store Nomos 256-bit nullifiers, an SMT of $2^{256}$ leaves would have to be used regardless of the amount of nullifiers in the set. Note, however, that only non-empty leaves and the necessary internal nodes need to be stored. The presence or absence of the nullifier $0$ would be recorded in the leftmost leaf of index $0$, of the nullifier $1$ in the leaf at index $1$, and of the highest possible nullifier $2^{256}-1$ in the rightmost leaf at the same index. Whenever a nullifier is added to the set, the SMT leaf value at that index is switched to $1$, and the internal node and root values derived from that leaf are recalculated. For batch updates, all leaves are updated before the rest of the tree is recomputed.

Generating a proof of non-membership for a nullifier is as easy as retrieving the Merkle path to the relevant leaf. This path includes the leaf value of $0$ as well as all the internal node values required to form reconstruct the SMT’s root. Verifying the proof involves actually reconstructing the root and ensuring that it is identical to the public root of the nullifier set.

Analysis

A major advantage of the SMT structure is the ease with which it handles proofs of non-membership. Since non-membership of a nullifier is indicated by a default value in the tree, a proof of non-membership can be verified quickly in the same manner as a proof of membership. Due to the fixed depth of the tree, the proof size is constant, making the process predictable and scalable. Despite the large size of the tree, which represents every possible nullifier, it is only necessary to store the non-empty leaves and modified internal nodes on their Merkle path. The SMT’s simple structure and append mechanism also makes it simple to implement.

However, the SMT’s fixed depth makes its ZK circuit more complex, requiring 256 hashes for proofs relating to Nomos’ 256-bit nullifiers. This makes the SMT better suited for systems with large numbers of nullifiers and steady nullifier growth.

Indexed Merkle Trees

An Indexed Merkle Tree (IMT) is a type of Merkle tree whose leaf nodes maintain additional pointers, creating an ordered structure similar to a linked list. An IMT inserts leaves in a sorted way, with each leaf also including a pointer to the next-highest value leaf. The addition of this pointer allows for efficient range and adjacency checks, as well as batch inclusions and non-membership proofs.

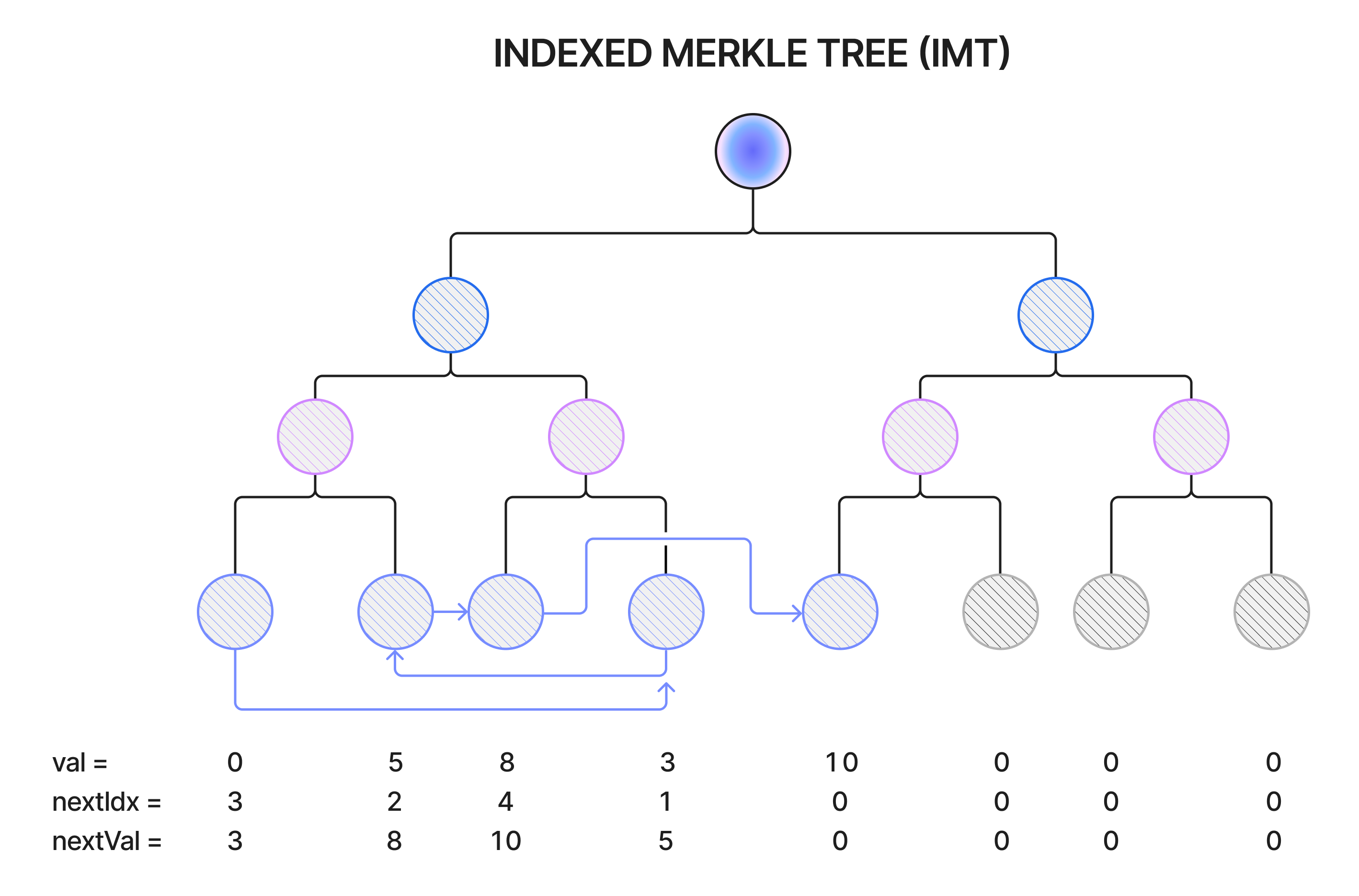
An IMT starts off with an empty tree of some arbitrary depth with, optionally, a “sentinel” node at index $0$ with a value of $0$, to which new leaf values are added. Proving non-membership in an IMT involves providing a Merkle path to the leaf holding the predecessor element, which is the largest element smaller than the element whose non-membership is being proven. The proof is verified by checking that this leaf points to a leaf with a value larger than the element under scrutiny.

To add a new nullifier to the tree, follow the instructions below:

1. Prove that the element to be inserted is not already in the tree, and that there is an empty leaf in the tree that can hold it. To find the predecessor element, iterate through the leaf nodes starting with the sentinel node and proceeding to the next-largest element to which it points in nextIdx. The largest element smaller than the nullifier to be inserted will be the predecessor element. For a modification of the IMT that allows for dynamic tree growth, see below.
2. Populate an empty leaf in the tree and update the pointers as in a linked list - that is, the leaf holding the predecessor element should point to the new leaf, and the new leaf should point to the leaf with the next-highest successor element (if it exists).
3. Recompute the hashes of the affected internal nodes and the IMT’s root.

As a result of this process, the leaf index represents the sequence in which the element was added to the tree, while the sorted list of elements is maintained by the pointers held by each leaf.

Unlike SMTs, IMTs support efficient batched updates by leveraging the leaves’ adjacency pointers. Instead of independently updating each nullifier, the algorithm finds the range of nullifiers affected and updates the structure in a grouped operation. A batch update largely proceeds according to the steps detailed above, except that the inserted elements are sorted and grouped into a subtree, which is then inserted instead of an empty subtree in the IMT of the same size.

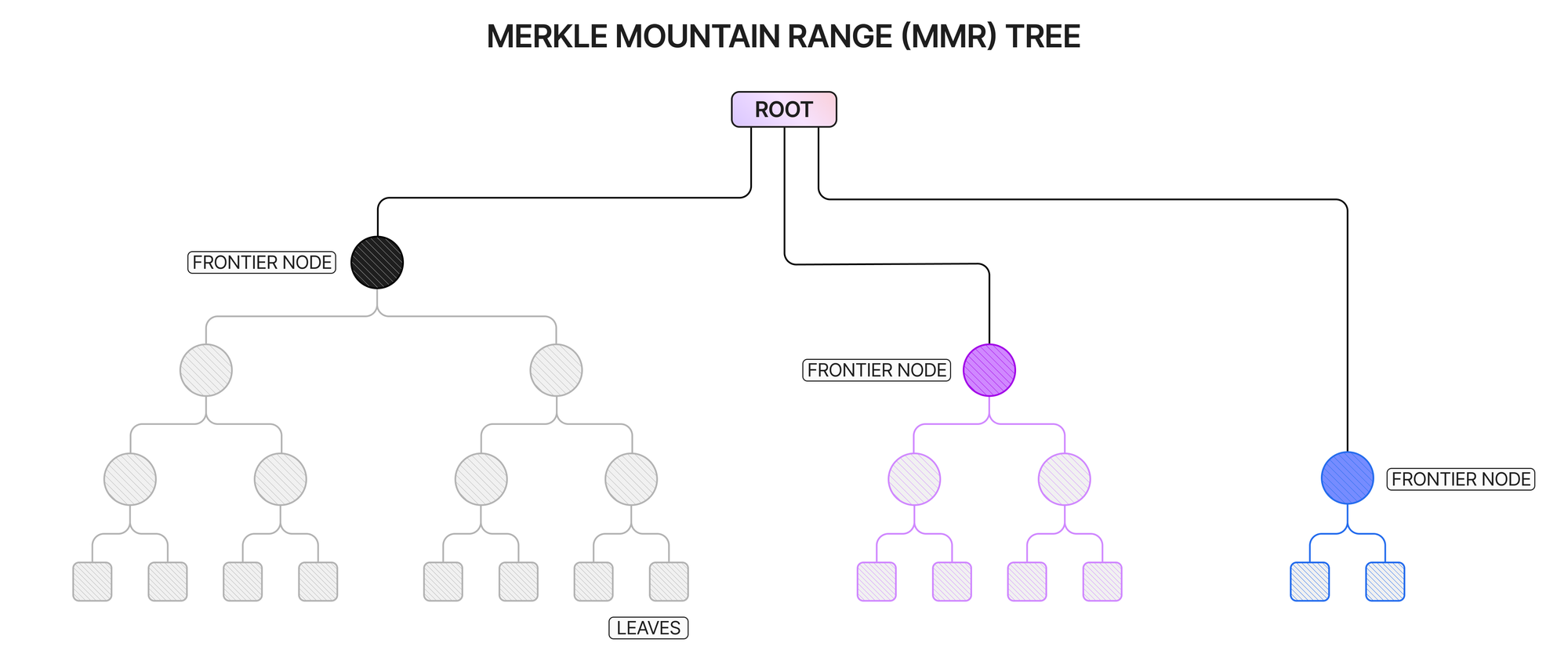
Dynamic Tree Growth with MMR IMTs

To allow for a nullifier IMT to grow dynamically, the IMT insertion process can be modified to incorporate qualities of the Merkle Mountain Range (MMR) tree. An MMR tree arranges the data into a set of the largest possible full binary Merkle trees, whose roots are then hashed together to create the tree’s root. Growing an IMT according to this design involves adding the subtree constructed of the new nullifier leaves, merging it with another subtree of the same depth if one is found. The root is then calculated as the hash of the concatenation of the roots of the subtrees, known as frontier nodes, and the adjacency pointers are updated to reflect the correct ordering of the nullifier values.

Analysis

A distinguishing feature of IMTs is their ability to represent elements in a set in fairly compact and dynamic way. Unlike SMTs, which operate within a fixed 256-bit namespace regardless of the size of the set, IMTs grow dynamically with the number of nullifiers. This dynamic structure eliminates the inefficiencies of managing a vast, sparsely populated tree, making IMTs a more efficient and compact choice for systems with smaller nullifier sets. The smaller tree size also has the effect of reducing the size of the non-membership proof, as well as the complexity of the ZK circuit.

On the other hand, handling adjacency pointers and the dynamic growth structure makes IMTs harder to implement, and the ZK circuit must accommodate the maximum subtree size possible for a batch update. Additionally, sorting elements for batch updates must be handled outside of the circuit, and storage requirements for an IMT are greater to accommodate the adjacency pointers.

Why MMR IMTs?

Ultimately, the Nomos team settled on Indexed Merkle Trees with the Merkle Mountain Range expansion mechanism as the structure of choice for zone nullifier sets. This is primarily because the set of nullifiers in a zone is not expected to exceed $2^{64}$ nullifiers. While SMTs prioritise simplicity and predictable performance, this comes at the cost of greater proof computation complexity due to their fixed depth. Therefore, they are not ideal for small datasets.

IMTs, on the other hand, have more efficient proofs due to their smaller depths. With the MMR growth mechanism, they can grow dynamically if necessary to accommodate more nullifiers than originally expected. Despite the implementation difficulty arising from pointer management and the extra memory required to store the tree elements, MMR IMTs’ computational efficiency and dynamic growth make them a superior choice for smaller nullifier sets. In any case, the complexity of insertions into an IMT are mitigated due to their efficient batch insertion algorithm.

Sources and Further Reading

• Indexed Merkle Tree (Nullifier Tree) - Aztec Network