NomosDA

Inner Product Arguments for Data Availability

IPAs have been proposed for use in data availability sampling due to several key advantages over the more popular KZG scheme.

Nomos Team

Nov 22, 2024 • 8 min read

Part 3 of a Series on Polynomial Commitment Schemes for NomosDA. Read Part 1 here and Part 2 here.

An Inner Product Argument (IPA) is an argument of knowledge scheme that uses Pedersen commitments to create commitments to polynomials. This scheme was introduced in a 2016 paper and refined in a 2017 paper by some of the same co-authors for use in Bulletproof ZK proofs. More recently, IPAs have been proposed for use in data availability sampling due to several key advantages over the more popular KZG scheme - namely, their transparent setup and relatively simple mathematical basis. As before, we will describe how the scheme works, followed by an analysis based on our criteria from Part 1.

How IPAs Work

Building Blocks

Before we can describe how IPAs work, it is crucial to understand their two primary “building blocks” - inner products and Pedersen commitments. An inner product is an operation involving two vectors where each element in one vector is multiplied by its corresponding element in the second vector, and the results are added up. In other words, for vectors $\vec a=\begin{bmatrix} a_0 & a_1 &\dots & a_{n-1} \end{bmatrix}$ and $\vec b=\begin{bmatrix} b_0 & b_1 &\dots & b_{n-1} \end{bmatrix}$ of the same length $n$, their inner product is defined as:

$$ P=\vec a \cdot \vec b=\sum_{i=0}^{n-1}a_ib_i $$

A Pedersen commitment is a relatively simple commitment that is built using the inner products of a vector of scalars and a vector of elliptic curve points. Like the KZG scheme, the Pedersen scheme relies on the difficulty of the generalised discrete logarithm problem for elliptic curves to ensure that a commitment cannot be falsified. Before a commitment can be created, the parties involved agree on a public vector of elliptic curve points $\vec G=\begin{bmatrix} G_0 & G_1 &\dots & G_{n-1} \end{bmatrix}$, known as the basis, which can be generated by any party. The length $n$ of this basis determines the maximum degree ($n-1$) of the polynomials that can be committed to with this setup.

For a polynomial $f(x)$ with coefficients $f_i$, a Pedersen commitment is created by computing the inner product of the vector of coefficients $\vec f=\begin{bmatrix} f_0 & f_1 &\dots & f_{n-1} \end{bmatrix}$ with $\vec G$, as follows:

$$ C=\vec f \cdot \vec G=\sum_{i=0}^{n-1}f_iG_i $$

The resulting commitment $C$ is an elliptic curve point on $\mathbb{G}$. Note that the public curve points in $\vec G$ require no trusted setup phase or secret generation, only requiring that a scalar $q$ is not known to the prover or verifier such that $G_i=qG_j$ for any points in the basis. This stands in contrast to KZG’s use of multiparty computation to generate the public set of elliptic curve points.

In its basic form, a Pedersen commitment is not very useful for data availability applications, since providing a proof for an evaluation $f(u)=v$ requires the prover to send all the coefficients $f_i$ to allow the verifier to compute the commitment and verify that it is correct. With a proof size of $\mathcal{O}(n)$, this is no better than just evaluating the polynomial directly.

Inner Product Arguments

Instead, we will create a commitment to $f(x)$ in the form of an inner product argument. Essentially, the goal is to create Pedersen commitments to show that the prover knows a coefficient vector $\vec f$ and a vector of the input powers $\vec u=\begin{bmatrix} 1 & u & u^2 &\dots & u^{n-1} \end{bmatrix}$, as well as the evaluation $v=f(u)$. In our case, where $\vec u$ is known to both the prover and verifier, there is no need to create a commitment to this vector. Additionally, while the IPA scheme can include a blinding factor to ensure that information apart from the selected evaluation is not revealed to the verifier, this is not an important property for data availability sampling since there is no need to hide the polynomial coefficients. Therefore, this factor will therefore be left out of the explanation that follows.

Each commitment naturally will have its own corresponding vector of curve points serving as its basis. These commitments are:

$$ F=\vec f\cdot \vec G\\ V=vQ=(\vec f\cdot\vec u)Q $$

where $\vec G$ is the public vector of elliptic curve points and $Q$ is a single elliptic curve point serving as the basis for the scalar evaluation $v$. $F$ is provided as the initial commitment to the polynomial, and $V$ is generated only once the verifier has sent their input $u$ for evaluation. Note that calculating $f(u)$ is equivalent to calculating the inner product of the coefficients and the corresponding powers of $u$.

$Q$ in this case is not a public point, but rather is generated randomly by taking the hash of the public data in the protocol. This procedure simulates, in a non-interactive way, the input of a random value from the verifier (as per the Fiat-Shamir heuristic). The reason for this randomness is to prevent a scenario where $Q$ is public, and a dishonest attacker provides an incorrect Pedersen commitment $F'=\vec f\cdot\vec G+\alpha Q$, for some scalar $\alpha$. Then, the prover could “prove” that $f(u)=v-\alpha$.

Now, due to the homomorphic property of elliptic curve points, the resulting commitments can be combined into one commitment, as shown below:

$$ \\ C=F+V \\=\vec f\cdot \vec G +(\vec f\cdot\vec u)Q $$

This commitment still suffers from the issues faced by the simple Pedersen commitments mentioned earlier, with one major difference - there is a way to create a reduced commitment that will be valid if and only if the original commitment is valid. This reduction process can be repeated until the final commitment has vectors of length $1$, dramatically reducing the proof size.

Argument Reduction

When we reduce $C$ to an equivalent commitment $C'$ that is, for instance, half its size, we must make sure that the reduced commitment retains the original’s structure. This structure can be thought of as a sum of a Pedersen commitment to a vector (in place of $\vec f$) and another commitment to an inner product of this vector with another vector (in place of $\vec f\cdot\vec u$). The lengths of these vectors must be an identical power of $2$ to allow for the reduction process to be repeated (see below). If the data has a different length, the vectors can be padded with zeroes to give them the desired lengths.

This reduction is accomplished by first splitting each vector in the original commitment into two halves in some consistent way. Then, the prover calculates two new “half-sized” commitments based on the structure of $C$ but using inner products of vectors from “opposite” halves. The prover continues by generating a random scaling factor $w$ by taking the hash of the public data. This factor is then used to generate the reduced vectors and the reduced commitment $C'$.

For this example, let us define the two halves as the odd- and even-indexed elements in each matrix, and group the “odds” and “evens” together into separate matrices. Then, our odd and even commitments $C_o$ and $C_e$ will be calculated as follows:

$$ C_o=\vec f_e\cdot\vec G_o+(\vec f_e\cdot\vec u_o)Q \\ C_e=\vec f_o\cdot\vec G_e+(\vec f_o\cdot\vec u_e)Q $$

Now, using the scaling factor $w$, we define the reduced vectors and bases of $C'$ as follows:

$$ \vec f' = w\vec f_e + w^{-1} \vec f_o \\ \vec u' = w^{-1}\vec u_e + w \vec u_o \\ \vec G' = w^{-1}\vec G_e + w \vec G_o $$

Finally, we calculate the reduced commitment:

$$ C'=w^2C_o+C+w^{-2}C_e $$

To see that $C'=\vec f'\cdot \vec G' +(\vec f'\cdot\vec u')Q$ holds, simply expand and regroup the terms on the left hand side:

$$ C'=w^2C_o+C+w^{-2}C_e \\ =w^2(\vec f_e\cdot\vec G_o+(\vec f_e\cdot\vec u_o)Q) \\ + \vec f_e\cdot\vec G_e+\vec f_o\cdot\vec G_o+(\vec f\cdot\vec u)Q \\ +w^{-2}(\vec f_o\cdot\vec G_e+(\vec f_o\cdot\vec u_e)Q) \\ = w^2f_e\cdot\vec G_o+\vec f_e\cdot\vec G_e+\vec f_o\cdot\vec G_o+w^{-2}\vec f_o\cdot\vec G_e\\+(w^2(\vec f_e\cdot\vec u_o)+\vec f_e\cdot\vec u_e+\vec f_o\cdot\vec u_o+w^{-2}(\vec f_o\cdot\vec u_e))Q \\ =(w^2f_e+f_o)\cdot(w^{-2}G_e+G_o) \\+(w\vec f_e+w^{-1}\vec f_o)\cdot(w^{-1}\vec u_e+w\vec u_o)Q $$

Factoring out $w$ and $w^{-1}$ from the first term allows us to plug in our reduced vectors and bases:

$$ = w(wf_e+w^{-1}f_o)\cdot w^{-1}(w^{-1}G_e+wG_o) \\+(\vec f'\cdot\vec u')Q \\ = \vec f'\cdot\vec G'+(\vec f'\cdot\vec u')Q $$

which would make it equivalent to the original equation defining $C$. This reduction process can be repeated, progressively halving the vectors used to create the commitment until they reduce to vectors of length $1$ - that is, individual scalar or elliptic point elements.

The Final Stage

In the final stage of the reduction process, the commitment is defined as follows:

$$ C^{end}=f^{end}G^{end}+f^{end}u^{end}Q $$

where $f^{end}, u^{end}$ are scalars and $G^{end},Q$ are elliptic curve points. The prover can thus send the verifier the proof $((C_o, C_e), (C_o', C_e'), (C''_o, C_e''), ..., f^{end})$, which has a length of $2\log(n)+1$ - a major improvement over the basic Pedersen proof size of $n$.

The verification process, during which the verifier will calculate the reduced bases $G'$ and the reduced vector $\vec u'$, entails the verifier repeating the reduction process to reach the final stage. At this point, they can plug in $f^{end}$ and verify the equation. Note that the reduction process can also be optimised using multiscalar multiplication techniques such as the Pippenger algorithm.

Vitalik’s IPA DAS Proposal

In a 2022 post on the Ethereum Research forum, Vitalik Buterin introduced an unusual way to use IPAs for data availability sampling. Because IPA proofs cannot be combined, the naïve way involves creating a polynomial commitment to the data directly and generating an independent proof for every chunk. Instead, Vitalik proposed to create a binary tree of commitments to portions of the data, with every commitment node for $m$ chunks having two children that are each commitments to one half of the chunks in their parent. At the top, the parent node is a commitment $C_{full}$ to the entire data, organised into chunks. At the bottom, the leaves of this tree are simple commitments to one chunk each. This is known as the proof tree, and it looks something like this:

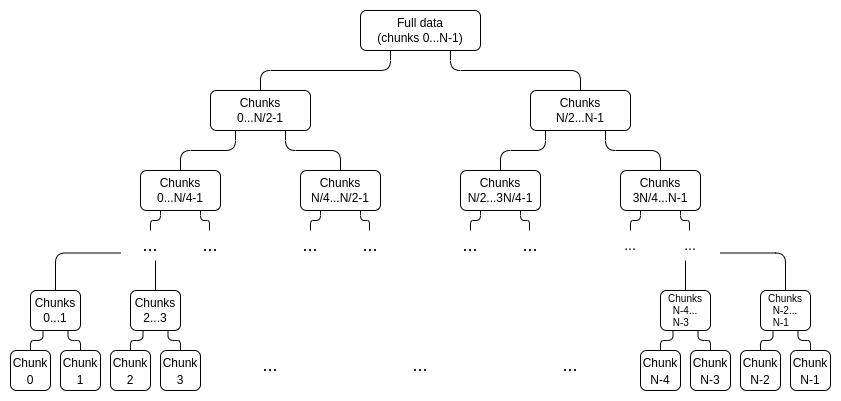
Source: https://ethresear.ch/t/what-would-it-take-to-do-das-with-inner-product-arguments-ipas/12088

In this scheme, the proof for any evaluation consists of the IPA commitment $C_u$ to that specific chunk together with its proof, as well as the highest-level commitments that can be added to $C_u$ to yield $C_{full}$, together with their associated proofs. The commitments selected here, representing parents of subtrees that can be combined with $C_u$, are reminiscent of the elements used in Merkle proofs.

To verify a proof in Vitalik’s scheme, the verifier must check every individual proof with the procedure described above, and also make sure that the sub-commitments it was provided add up to the top-level commitment to the entire data. This ultimately results in a proof time of $\mathcal{O}(n\log(n))$ and verification time of $\mathcal{O}(n)$ - with the major advantage being that multiple proof verifications can be batched together. It should be noted that Vitalik ultimately rejected this scheme in favour of KZG for Ethereum Danksharding.

Analysis

With a transparent setup and using just basic elliptic curve operations, IPAs have an advantage compared to the trust assumptions and mathematical complexity of KZG. Just like KZG, several commitments can be combined into a single constant-size commitment through simple elliptic curve point addition. However, proving an evaluation and verifying a proof both take $\mathcal{O}(n)$ time, while the proof size is non-constant at $\mathcal{O}(\log(n))$. In Vitalik’s proposal for the use of IPAs for data availability, the proof generation time balloons to $\mathcal{O}(n\log(n))$. Additionally, just like the KZG scheme, IPAs are not post-quantum secure.

Sources and Further Reading