Ensuring data availability - the guarantee that blockchain data is available for download - is a critical challenge for modern decentralized systems where scalability is paramount. NomosDA, the data availability scheme used by the Nomos network, addresses this challenge by providing a mechanism that guarantees that all data from Nomos zones - referred to as blobs - are accessible and verifiable by every network participant. This article delves into the motivations behind NomosDA’s development and provides an in-depth overview of its operational framework.

Design Principles

Data Availability (or DA) in the context of the Nomos network is the assurance that the entire blob data is public and can be downloaded if desired by any participant in the network. While DA can be easily accomplished by having each node keep copies of entire blobs, this solution introduces serious limitations on scaling and makes implementing light nodes impossible.

Instead, NomosDA uses Data Availability Sampling (DAS) to convince nodes of the completeness of the data. DAS involves each node making several samples of the data, which is first encoded with an error-correcting code. Because of the properties of this encoding, a malicious party intending to prevent the reconstruction of the data must withhold a very large proportion of the encoded data. Therefore, even a few samples on the encoded data will determine with a very high degree of confidence whether any portion of the original data was excluded. DAS provides an assurance of data availability at the time the sampling client verifies the relevant proofs, but not for any time after that.

While there is a great variety of DA schemes available today, the Nomos project is unique enough to require its own, purpose-built DA solution. More specifically, NomosDA was engineered to work best with the following features of the Nomos network:

• Decentralization: For Nomos, decentralisation is critically important. Therefore, permissioned DA schemes involving a Data Availability Committee (DAC) were avoided. Schemes that require some nodes to download the entire blob data were also off the list due to the disproportionate role played by these “supernodes”.
• Scalability: NomosDA was designed to minimise the amount of data sent to DA nodes, reducing the communication bottleneck and allowing more nodes to participate in the DA process. Based on our research, we have concluded that splitting the data into several columns, each sent to a different group of nodes, best facilitates this process. The initial NomosDA design splits the data into 2048 columns, but this number is expected to grow as the network scales.

Overview

NomosDA involves three different kinds of network participants, each with their own unique role. These are:

• Zone Executors: Executors are Nomos validators that choose to also provide validation services to one or more zone(s). They are the ones that prepare the zone data for DA and distribute it to participating nodes.
• Validators participating in DA: These nodes, referred to as participating nodes for short, receive portions (”columns”) of the data from executors and verify that their column was encoded correctly. This proof is then combined with those from participating nodes working on other columns to ensure the integrity of the entire data. These nodes are organised into 2048 groups called subnets, each responsible for one column.
• Light Nodes: Light nodes can be run with minimal software requirements and allow anyone to engage in the DA sampling process. They send requests to sample the data at several random points and verify that the data is available and encoded correctly.

The process via which these participants interact can be described as involving two distinct stages: Encoding and Dispersal. Additionally, Reconstruction can be invoked as a third stage in the scenario where some of the data is found to be unavailable.

Benchmarks

In order to facilitate scalability, as described in the previous section, the NomosDA design has to be be able to perform its three stages relatively quickly. While a full analysis of NomosDA’s performance is outside the scope of this post, a few key metrics will be briefly mentioned below. All results are for a relatively large 1 MB blob split into 2048 columns:

• Encoding, due to requiring many proof computations, is by far the most time-consuming stage. With NomosDA, it takes 11.96 s to encode a 1 MB blob in the worst case.
• Verification is fairly fast, taking only 71.36 ms in the worst case.
• Reconstruction is exceptionally fast with NomosDA, taking only 3.39 ms in the worst case to reconstruct the entire blob with 50% of the chunks missing.

Tests for verification and reconstruction were run on a machine with the following specifications:

• Processor: Intel Core Ultra 7 155H (16 Cores 22 Threads) @4.8GHz
• RAM: 32GB DDR5-4800

Meanwhile, the tests for encoding, which are expected to be run by executors with bigger machines than those used by participating nodes, were run on a machine with the following specifications:

• Processor: AMD Ryzen 9 7950X3D (16 cores/ 32 threads) @4.2 GHz
• RAM: 128GB DDR5 (Memory footprint of ~8GB)

Encoding

Encoding is the first stage of the NomosDA process, in which a zone executor takes the original zone data and converts it into a form compatible with DAS. This encoding process involves the use of cryptographic protocols known as polynomial commitments and error-correcting codes. These protocols are used to transform the data to allow it to be split up and verified for availability in the dispersal phase.

Before encoding can begin, the data must be arranged into a matrix of 31-byte data chunks. Each chunk has 31 bytes rather than 32 to ensure that the chunk value does not exceed the maximum value on the BLS12-381 elliptic curve. The chunks are arranged into rows \(k=1024\) chunks long, and the 1024 columns of the matrix are each \(\ell\) chunks long. Visually, this matrix can be represented in the form shown below:

Once this is done, encoding the data for NomosDA can begin. This process consists of four steps:

1. Calculating the Row Commitments
2. Expanding the Rows and Calculating the Row Proofs
3. Calculating the Column Commitments
4. Computing the Aggregate Column Commitment and Column Proofs

Calculating Row Commitments

The first step in the encoding process is to calculate KZG polynomial commitments to each of the rows in the data blob. To do this, each chunk in the matrix is interpreted as a 31-byte element in the scalar finite field used for the BLS12-381 elliptic curve. For a detailed overview of the KZG commitment scheme, see here.

For each row \(i\), a unique 1023-degree polynomial \(f_i\) is generated such that each chunk \(data_i^j\) is the result of the evaluation \(f_i(\omega^j)\), where \(\omega\) is a 1024th root of unity (i.e. an element \(\omega\) such that \(\omega^{1024}=1\)) of the scalar field. Then, using previously-generated global parameters, 48-byte KZG commitments \(r_i\) are generated for each row’s polynomial.

Expanding the Rows and Calculating the Row Proofs

At this stage, the zone executor will expand each row using Reed-Solomon erasure coding. Known as RS coding for short, this error-correcting code is based on the fact that any \(n\)-degree polynomial can be uniquely determined by \(n+1\) points satisfying the polynomial equation. In our case, each row polynomial \(f_i\) is uniquely determined by the set of points

$$ \{(\omega^j, data_i^j)|\forall j\in\{0,...,1023\}\} $$

RS coding involves expanding this set of points to a larger set, all of which are points on the row polynomial \(f_i\). The factor by which each row is expanded is known as the expansion factor, which, for the purposes of NomosDA, is \(2\). This means that the zone executor must double the original data set by calculating the points

$$ \{(\omega^j,f_i(\omega^j)|\forall j\in\{1024,...,2047\}\} $$

The motivation for using RS coding is to make it much more likely to determine, via DAS, whether any data has been withheld. Since any 50% of the expanded row data can be used to determine the row polynomial and therefore to reconstruct the rest of the row data, preventing reconstruction would require withholding at least 51% of the expanded chunks. This allows a sampling client to detect whether data has been withheld with very few samples.

Visually, we can represent this step as a doubling of the column numbers in the data blob while keeping the row numbers constant:

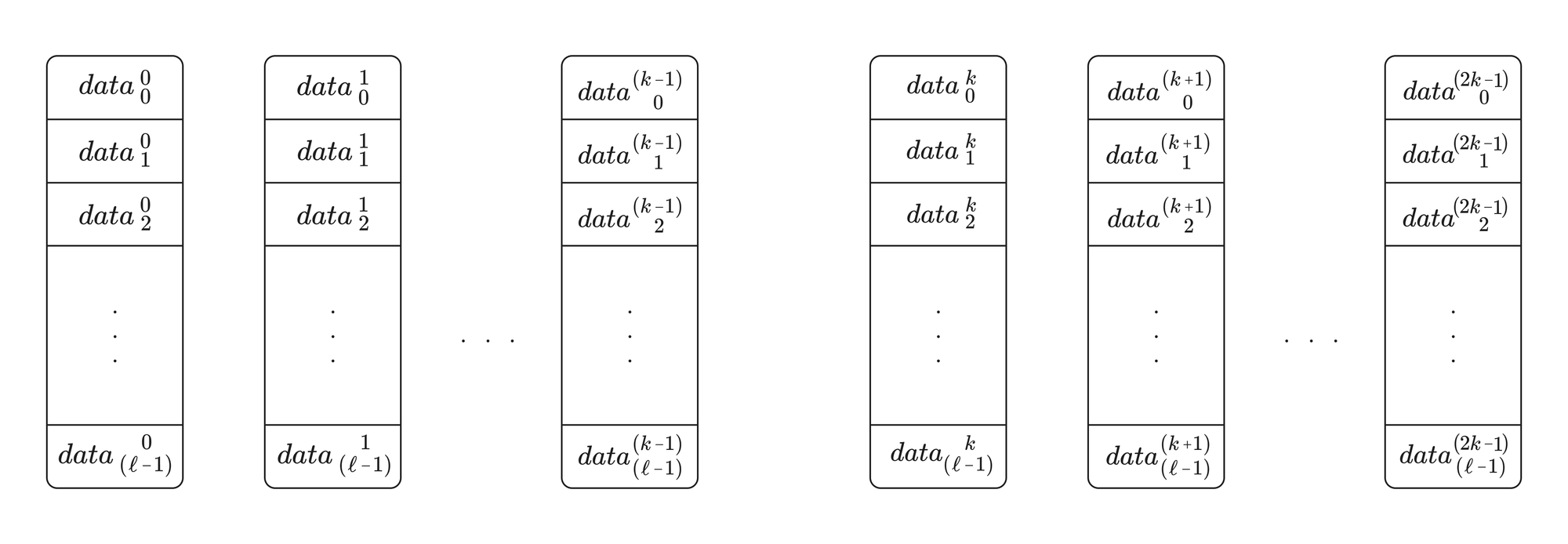
Another convenient property of RS coding is that, since the expanded data chunks in each row are just extra points satisfying the same row polynomial \(f_i\), the row commitments calculated in the previous step on the original rows will be identical to the commitments to the expanded rows. Once the rows are expanded, the zone executor also generates KZG proofs for each chunk.

Calculating the Column Commitments

Once the data chunk is expanded and the proofs are calculated, the zone executor can begin to calculate the column commitments. This is done in the same manner as the row commitments, using KZG:

1. First, find an \(\ell-1\) degree polynomial \(\theta_j\) defined by the data chunks in the column, such that \(\theta_j(\omega^j)=data_i^j\), where \(\omega\) is a generator of the field.
2. Then, use the KZG scheme to calculate commitments \(C_j\) for each \(\theta_j\).

Computing the Aggregate Column Commitment and Column Proofs

The final stage of the encoding process is the calculation of the aggregate column commitment. In this case, the hashes of the column commitments \(C_j\) are used as a data vector that defines a unique degree 2047 polynomial \(\Phi\). The hashes of the column commitments are used instead of the commitment values themselves to ensure that the polynomial evaluations remain in the 31-byte scalar field, rather than the 48-byte elliptic curve base field. Once \(\Phi\) is found, in the same manner as described above, it is used to calculate the aggregate column commitment \(C_{agg}\). The zone executor also generates proofs for the hash values of every column commitment.

Dispersal

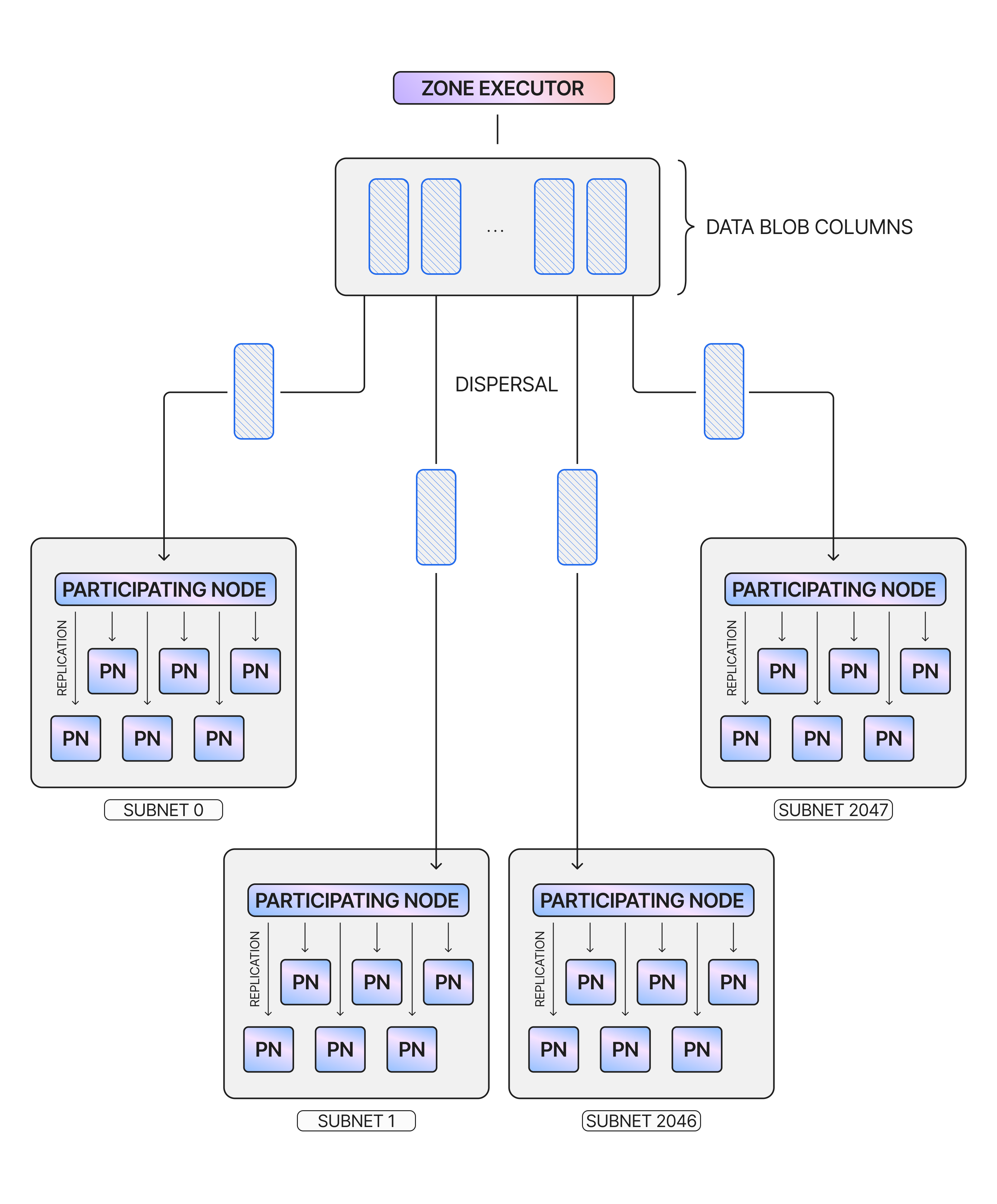
Once the data blob is correctly encoded and split into columns for data availability, the next step in the NomosDA process is to distribute it to Nomos nodes participating in DA. This is known as the Dispersal phase. Each node belongs to a subnet, which determines the portions of the blob that it receives. The zone executor that encoded the data also publishes the data commitments from the previous stage, allowing any node to engage in data availability sampling.

In NomosDA, validator nodes participating in the DA process are known as participating nodes. At the beginning of each epoch, each node is typically assigned to one of 2048 groups, known as subnets. If there are very few available participating nodes, each node could be assigned to multiple subnets.

During the dispersal phase, the zone executor will select one node in each subnet and send it the associated column of the encoded data blob. The node will also receive the various commitments and proofs required for the verification of data availability (see below). If there are multiple nodes in a subnet, the node that received the column will then replicate that data to all the other nodes in the subnet. This way, every participating node only downloads one column of the data blob, and every subnet is responsible for its own column. As will be described below, each participating node will then verify its own column data and receive assurances from the other subnets’ nodes about their columns’ veracity.

The dispersal and replication process can be visualized as in the diagram below:

Verification

When a node receives the column data for column \(i\), it also receives the commitments and proofs required to verify the column data. These are, for each row \(i\):

• The row commitments \(r_i\)
• The row proofs of the chunks in the column \(\pi_{r_i}^j\)
• The column commitment \(C_j\)
• The aggregate column commitment \(C_{agg}\)
• The proof of the hashed value of the column commitment \(\pi_{C_j}\)

With this information, the node is ready to verify the data. It performs a series of checks, all of which must pass for the node to certify that the column data is correct.

First, the node checks whether \(C_j\) was calculated correctly by the zone executor. This is done by interpolating a unique polynomial over the column data and calculating its KZG commitment, just as described in the Encoding section. If this commitment matches \(C_j\), then the column commitment is correct. This check ensures that the order of the rows in the data chunk square has not been tampered with.

Then, the node calculates the hash value of \(C_j\) and, using \(C_{agg}\), verifies \(\pi_{C_j}\). If this proof is found to be valid, then the node can be sure that the columns in the data chunk square have not been reordered, and that no columns have been added.

After that, the node verifies the proofs \(\pi_{r_i}^j\) for each row, using the commitments \(r_i\) and the column data. This check ensures that the order of the chunks in each row has not been changed.

If all the verification checks have passed, the node will send a message to the executor acknowledging that the column was verified. Once the executor has collected enough messages to reach the minimum threshold value, then there is an assurance that the data is available and has not been tampered with.

Data Availability Sampling

After the blob columns are dispersed to all participating nodes, any party can engage in data availability sampling to verify the availability of the entire data. In particular, Nomos nodes will use DAS to verify a blob when building a block that includes a blob-carrying transaction, or when verifying a block with blobs that was just recently proposed. DAS is also used by light nodes, enabling anyone to participate in ensuring the integrity of the blob data. Unlike regular nodes, NomosDA light nodes download much less data, allowing them to be run with minimal hardware requirements.

In NomosDA, a sampling client will select several random row and column values and send a request to participating nodes from the subnets corresponding to the chosen column values. These participating nodes will send the chunk values at the selected coordinates back to the sampling client. As part of the dispersal process, the zone executor responsible for the data blob publishes the row, column, and aggregate column commitments and proofs to the mempool. Once the commitments and proofs are included in a block, the sampling client can query this data and, together with the downloaded chunks, verify the availability of the entire data.

Verification

A node engaging in DAS will select a series of row and column coordinates, corresponding to the chunks it wishes to sample. For each row and column pair \((i,j)\), it will send a request for data from a participating node corresponding to the column it wishes to sample. This node sends the node engaging in DAS the data chunk \(data_i^j\) as well as a proof for the chunk data with respect to its column \(\pi_{data_i^j}\), while the node engaging in DAS pulls the following information from the chain:

• The row commitment \(r_i\)
• The proof of the data chunk \(\pi_{r_i}^j\)
• The column commitment \(C_j\)
• The aggregate column commitment \(C_{agg}\)
• The proof of the hashed value of the column commitment \(\pi_{C_j}\)

In a similar fashion to the verification process in the Dispersal phase described above, the node calculates the hash value of \(C_j\) and, using \(C_{agg}\), verifies \(\pi_{C_j}\). It then verifies the proof \(\pi_{r_i}^j\), using the commitment \(r_i\) and the data chunk \(data_i^j\). Finally, the node verifies the proof \(\pi_{data_i^j}\) using \(C_j\).

If all these checks pass, the sampling client is assured that the data it sampled is encoded correctly.

Reconstruction

The Reconstruction phase is intended as a fallback mechanism, allowing clients to have access to zone data even if it is being withheld by the active executor. Any party that wants to download the entire blob data and discovers that some portion of the blob is unavailable can invoke the reconstruction procedure to recover the missing data. In the scenario where the only missing chunks are in the “right half” of the row (indices \(j=k\) to \(2k-1\)), the original data can be found intact in the “left half” of the row (indices \(j=0\) to \(k-1\)). However, if there are missing chunks in the left half, the Reed-Solomon erasure code that was used to encode the data can also be used to reconstruct it. This works so long as the missing portion is not more than 50% of the total data.

As mentioned in the Encoding section, the polynomial \(f_i\) that fit the original \(k\) chunks in every row \(i\) is uniquely determined by any \(k\) chunks taken from the \(2k\) encoded chunks in that row. Therefore, a client engaging in reconstruction will first sample at least \(k\) available chunks in a given row. The client will use these chunks to interpolate the unique \(k-1\) degree polynomial that fits the points \((\omega^j,data_i^j)\) for every index \(j\) where the chunk is found to be available. Then, evaluating this same polynomial for inputs \(\omega^j\) for the remaining indices in the “left half” (\(0\leq j<k\)) will produce the missing data chunks.

Conclusion

NomosDA was created as a tailor-made solution to the data availability problem on the Nomos network. By leveraging cryptographic techniques like Reed-Solomon coding and polynomial commitments, NomosDA uses Data Availability Sampling to ensure that blob data is accessible, verifiable, and tamper-proof without compromising scalability or decentralisation. This unique approach not only facilitates efficient validation across the network but also empowers light nodes to participate in the verification process, strengthening the integrity of the entire system.

Sources and Further Reading

• Description and architecture - Nomos
• KZG Commitments for Data Availability
• Why We Chose KZG for NomosDA