KZG Commitments for Data Availability
The KZG scheme was designed to reduce communication costs. This scheme is therefore a popular choice for use in data availability layers.

Part 2 of a Series on Polynomial Commitment Schemes for NomosDA. Read Part 1 here.
The KZG (Kate-Zaverucha-Goldberg) commitment scheme is the original polynomial commitment scheme (PCS), introduced in a paper published in 2010. A major principle of this design, according to the co-authors, is to reduce communication costs; therefore, unlike previous homomorphic commitment schemes, KZG commitments and proofs are of a constant size. Since its introduction, this scheme has enjoyed great popularity in a variety of blockchain projects, especially for use in data availability layers. We will describe how the scheme works, followed by an analysis based on our criteria from Part 1.
How it Works
The KZG commitment scheme relies on a trusted pair setup that uses elliptic curve pairings, where several parties use multiparty computation to generate a secret scalar \(\tau\). This secret is used to calculate the following set of elliptic curve points, which are then made public:
$$ \{\tau^iG_1, \tau G_2 |\forall i \in \{0,...,d\}\} $$
where \(d\) is the degree of the polynomials to be committed to, \(G_1\) is the generator of a cyclic subgroup of the elliptic curve \(\mathbb{G}_1\) and \(G_2\) is the generator of a cyclic subgroup of the elliptic curve \(\mathbb{G}_2\), whose elements are in the extension field relative to the elements of \(\mathbb{G}_1\). After this initial stage, \(\tau\) is discarded and, due to the difficulty of the generalised discrete logarithm problem for elliptic curves, cannot be easily calculated from the publicly available points.
After the trusted setup, the KZG process can proceed as shown in the following diagram:
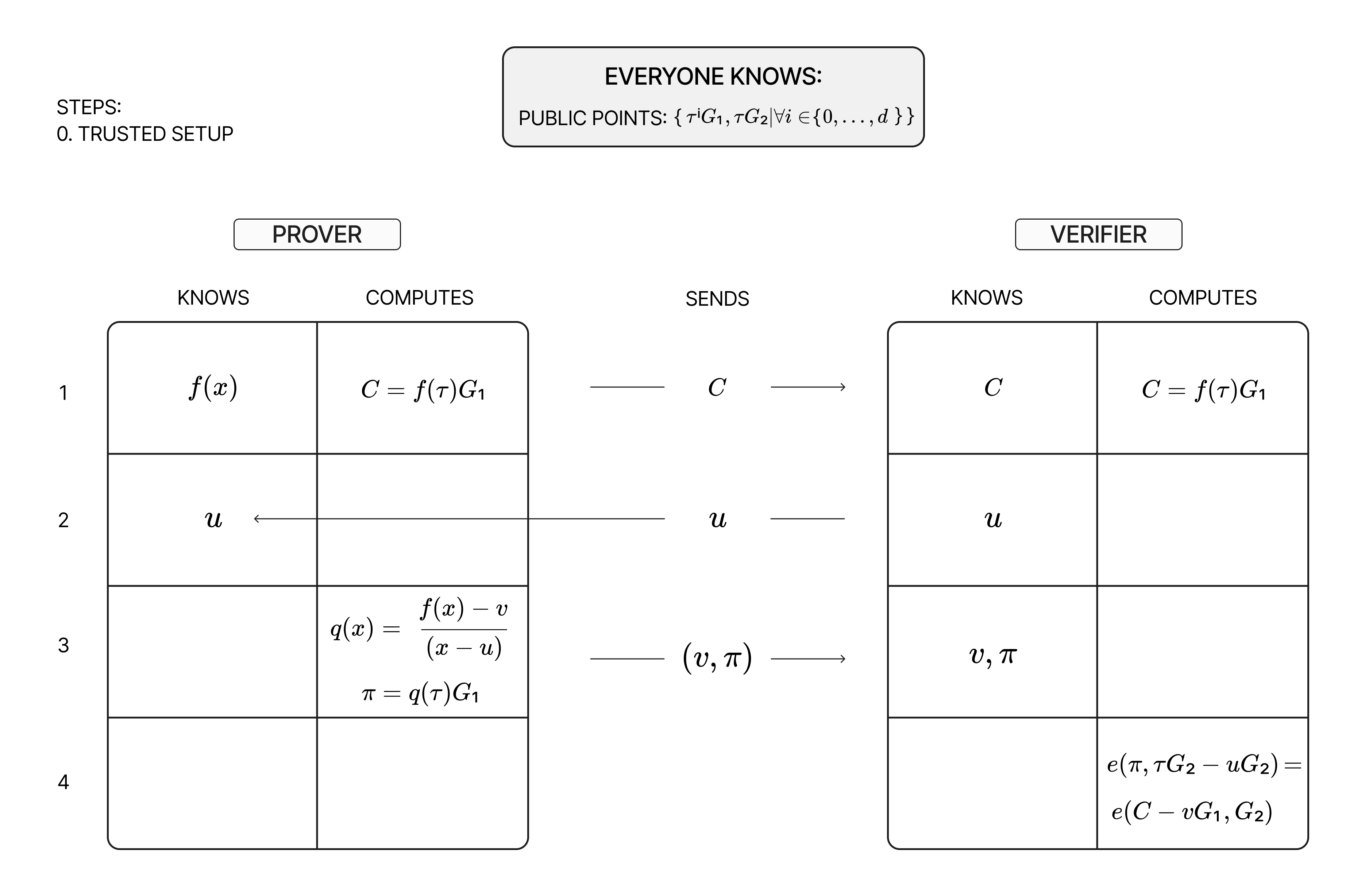
In Step 1, the prover calculates the commitment to some polynomial \(f(x)\) with coefficients \(f_i\) as follows:
$$ C=f(\tau)G_1=\sum_{i=0}^df_i\tau^iG_1 $$
Note that, while the prover does not know \(f(\tau)\), it knows the public points \(\tau^iG_1\) and can therefore calculate the commitment and send it to the verifier.
In Step 2, the verifier sends their desired input \(u\), and in Step 3 the prover can proceed to generate a proof \(\pi\) for their assertion that \(f(u)=v\) as follows:
$$ \pi=q(\tau)G_1 =\frac{f(\tau)-v}{\tau-u}G_1 $$
where \(q(x)=\frac{f(x)-v}{x-u}\) is known as the quotient polynomial. Intuitively, the quotient polynomial can only exist if \(f(u)=v\), in which case \(x-u\) will be a factor of \(f(x)-v\). The calculation of the proof \(\pi\) is accomplished using the public curve points, in the same manner as the calculation of the commitment. The prover finishes by sending \(\pi\) and \(v\) to the verifier.
Finally, in Step 4, the verifier is ready to check whether the prover’s claims about the evaluation of the polynomial are correct. At this point, they have received the commitment, claimed evaluation, and proof from the prover, and will seek to verify whether \(q(x)\) exists at any point. This is equivalent to checking the following equation at the particular point \(\tau\):
$$ q(\tau)(\tau-u)=f(\tau)-v $$
Verifying this equation is equivalent to verifying
$$ q(\tau)(\tau-u)e(G_1,G_2)=(f(\tau)-v)e(G_1,G_2) $$
where \(e()\) is an elliptic curve pairing defined over \(\mathbb{G}_1\) and \(\mathbb{G}_2\). Because of the bilinear property of elliptic curve pairings, this equation is equivalent to
$$ e(q(\tau)G_1, \tau G_2-uG_2)=e(f(\tau)G_1-vG_1,G_2) $$
Conveniently, the verifier knows most of these values from the prover’s calculations and can easily calculate the rest. The equation can therefore be rewritten as follows:
$$ e(\pi, \tau G_2-uG_2)=e(C-vG_1, G_2) $$
With all the values required to calculate the results of these two elliptic curve pairings, the verifier can easily see whether they are equal.
Proofs of Multiple Evaluations
An important property of the KZG scheme is its ability to create one constant-sized proof for any number of evaluations, not just one as above. Therefore, several evaluation proofs can be “batched” into the same size as a single evaluation proof, greatly reducing communication costs.
Creating a batched proof \(\pi'\) for \(k\) evaluations is very similar to the process for a single evaluation, albeit with more elliptic curve points generated in the trusted setup phase:
$$ \{\tau^iG_1, \tau^kG_2 |\forall i \in \{0,...,d\}, \forall k \text{ where } 0\leq k\lt d\} $$
In this case, \(k\) represents the maximum number of proofs to be batched together. The process also uses a slightly different quotient polynomial:
$$ \pi'=q'(\tau)G_1=\frac{f(\tau)-i(\tau)}{\prod_{j=0 }^{k-1}(\tau-u_j)}G_1 $$
where \((u_j,f(u_j))\) are the evaluation points and \(i(\tau)\) is a polynomial of degree \(k-1\) that is satisfied for all these points. Since this polynomial is derived via Lagrange interpolation, it is known as the interpolation polynomial.
Checking this proof is also a bit different. In this case, the verifier checks
$$ q'(\tau)(\prod_{j=0 }^{k-1}(\tau-u_j))e(G_1,G_2)=(f(\tau)-i(\tau))e(G_1,G_2) $$
This is equivalent to:
$$ e(\pi', (\prod_{j=0 }^{k-1}(\tau-u_j))G_2)=e(C-i(\tau)G_1, G_2) $$
As in the single evaluation case, the verifier knows or can calculate all of the values necessary to verify the proof.
Feist-Khovratovich Algorithm
Calculating a batched proof takes \(\mathcal{O}(n\log^2(n))\) time, which beats creating all the proofs individually in \(\mathcal{O}(nm)\) time. However, there is a way to create multiple individual proofs in \(\mathcal{O}(n\log(n))\) time, with some restrictions. This is method is known as the Feist-Khovratovich algorithm, and it only works if the \(k\) evaluations are powers of the \(k\)th root of unity (i.e. an element \(w\) such that \(\omega^k=1\)) of the scalar field associated with \(\mathbb{G}_1\) and \(\mathbb{G}_2\). Note also that \(k\) must be a power of \(2\) for the FK algorithm to work.
When calculating a quotient polynomial \(q(x)=\frac{f(x)-f(w^i)}{x-w^i}\), the coinventors of the FK algorithm noticed that its coefficients \(q_j\) can be derived recursively using the coefficients \(f_j\) of \(f(x)\), as follows:
$$ q_{d-1}=f_{d} \\ q_j=f_{j+1}+\omega^iq_{j+1}, \forall j\in[0,d-1) $$
If we expand each \(q_{j+1}\) term based on its definition in terms of the coefficients \(f_j\), we get the following:
$$ q_{d-1}=f_{d} \\ q_{d-2}=f_{d-1}+\omega^if_d \\ q_{d-3}=f_{d-2}+\omega^if_{d-1}+\omega^{2i}f_d \\ \vdots \\ q_0=f_1 + \omega^if_2 + \omega^{2i} f_3 + \dots + \omega^{(d-1)i} f_d $$
This allows us to simplify \(q(x)\) by grouping together all the terms with a common \((\omega^i)^j\) factor, as follows:
$$ q(x)=(f_dx^{d-1}+f_{d-1}x^{d-2}+\dots+f_1) \\ +(f_dx^{d-2}+f_{d-1}x^{d-3}+\dots+f_2)\omega^i \\ +(f_dx^{d-3}+f_{d-1}x^{d-4}+\dots+f_3)\omega^{2i} \\ \vdots \\ +f_d\omega^{(d-1)i} $$
Let’s call the polynomials multiplied by each power of \(\omega^i\) “\(h_j(x)\)”, ranging from \(j=0\) to \(d-1\). Now, observe that these polynomials can be represented as a result of a Toeplitz matrix product:
$$\begin{bmatrix}h_0 \\h_1 \\ \vdots \\h_{d-1}\end{bmatrix}= \begin{bmatrix} f_d & f_{d-1} & f_{d-2} & \dots & f_1 \\ 0 & f_d & f_{d-1} & \dots & f_2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & f_d \end{bmatrix} \begin{bmatrix} x^{d-1} \\ x^{d-2} \\ \vdots \\ 1\end{bmatrix} $$
Calculating this matrix product takes \(\mathcal{O}(n\log(n))\) time.
Now, we can represent \(q(x)\) as a sum of \(h_j(x)\omega^{ij}\), and therefore the proof for our evaluation \(\pi_i\) will be
$$ \pi_i=q(\tau)G_1=\sum_{j=0}^{d-1}h_j(\tau)w^{ij}G_1 $$
The main insight of the coinventors of the FK algorithm is that, if we put all the \(h_j(\tau)G_1\) proofs into a vector \(H=\begin{bmatrix} h_0(\tau)G_1 & h_1(\tau)G_1 &\dots & h_{k-1}(\tau)G_1 \end{bmatrix}\), then we can use the Discrete Fourier Transform to transform \(H\) into a vector of our desired evaluation proofs. Since, for some vector \(A=\begin{bmatrix} a_0 & a_1 &\dots & a_{2^n-1} \end{bmatrix}\),
$$ DFT(A)=\begin{bmatrix} \sum_{i=0}^{2^n-1}a_i & \sum_{i=0}^{2^n-1}a_i\omega^i & \sum_{i=0}^{2^n-1}a_i\omega^{2i} &\dots & \sum_{i=0}^{2^n-1}a_i\omega^{(2^n-1)i} \end{bmatrix} $$
Therefore, since \(k\) is a power of \(2\), we can calculate the Discrete Fourier Transform of \(H\), which is the same as calculating all \(k\) proofs.
$$ DFT(H)=\begin{bmatrix} \sum_{j=0}^{d-1}h_j(\tau)G_1 & \sum_{j=0}^{d-1}h_j(\tau)\omega^{j}G_1 &\dots & \sum_{j=0}^{d-1}h_j(\tau)\omega^{(k-1)j}G_1 \end{bmatrix} \\ = \begin{bmatrix} \pi_0 & \pi_1 &\dots & \pi_{k-1} \end{bmatrix} $$
Calculating the DFT of a vector takes \(\mathcal{O}(n\log(n))\) time. Therefore, the whole FK algorithm can calculate all \(k\) proofs in just \(\mathcal{O}(n\log(n))\) time.
Analysis
The KZG scheme is among the most popular commitment schemes, to the extent of being integrated into Ethereum ever since Proto-Danksharding was introduced. This makes it extremely simple to implement, given the wide variety of existing libraries and implementations available. KZG commitments and proofs are of a constant size \(\mathcal{O}(1)\), and verification time is also \(\mathcal{O}(1)\). Proving an evaluation can be done in \(\mathcal{O}(n)\) time, and calculating proofs for all the evaluations in the dataset takes \(\mathcal{O}(n\log(n))\) time using the Feist-Khovratovich algorithm. However, the KZG scheme relies on an initial trusted setup to calculate the initial set of elliptic curve points, and is not post-quantum secure.

