Private Proof of Stake with Ouroboros Crypsinous
Even though Private PoS appears to be a contradiction in terms, Ouroboros Crypsinous was able to make it work.

Part 2 of a series on the Ouroboros Family of Consensus Protocols. Read Part 1 here.
The Ouroboros consensus protocol was introduced in 2017 as the first provably secure Proof of Stake (PoS) system. Within the span of a few years, improvements on that original protocol, retroactively referred to as Ouroboros Classic, were produced by many of the same authors. These improved protocols, known as Ouroboros Praos and Ouroboros Genesis, extended the security guarantees of Ouroboros Classic to include scenarios with more powerful adversaries and limited connectivity between peers. These protocols have been accepted for practical use in the blockchain space, with the more recent iteration Ouroboros Genesis being the consensus mechanism used by Cardano at the time of writing. An introduction to Ouroboros Classic, Praos, and Genesis can be found in the previous instalment of this article series.
However, one important property that remained out of reach for these Ouroboros protocols was privacy. The idea of a privacy-preserving PoS consensus protocol even appears to be a contradiction in terms, as the leadership election necessarily relies on the knowledge of the relative stake each party holds. Despite this limitation, a privacy-preserving PoS protocol known as Ouroboros Crypsinous was created based on the Ouroboros model. This article will serve as an introduction to this protocol, explaining how it works and how it compares with its predecessors in the Ouroboros family.
How Ouroboros Crypsinous Works
Ouroboros Crypsinous, introduced in a 2019 paper, is the first formally analysed privacy-preserving PoS blockchain protocol. This formal analysis reflects Crypsinous’ legacy as a member of the Ouroboros family, which pioneered provable security for PoS systems. Crypsinoushas therefore been proven to be secure against adversaries that can corrupt any participant with some delay, known as adaptive adversaries. Like in Ouroboros Genesis, honest parties in Crypsinous are assumed to hold the majority of the stake and there is a maximum delay for message delivery which is unknown to honest parties.
The authors of the Ouroboros Crypsinous paper describe the protocol as combining the strengths of both Ouroboros Genesis, as well as private Proof of Work (PoW) blockchain protocol Zerocash. Crypsinous adopts the fork choice rule, forward-secure encryption, and general leadership election model from Genesis (with modifications), while implementing the private ledger in a way similar to that of Zerocash.
Just like Genesis, Crypsinous divides time into atomic units called slots which allow for the addition of at most one block, and groups several slots into longer periods called epochs. Each epoch is used to determine the randomness and eligibility set used in the election of block leaders. It also uses Genesis’ unique fork choice rule, selecting the longest chain for shallow forks and the densest chain for deep forks to ensure that honest parties can join or rejoin the protocol without trust assumptions.
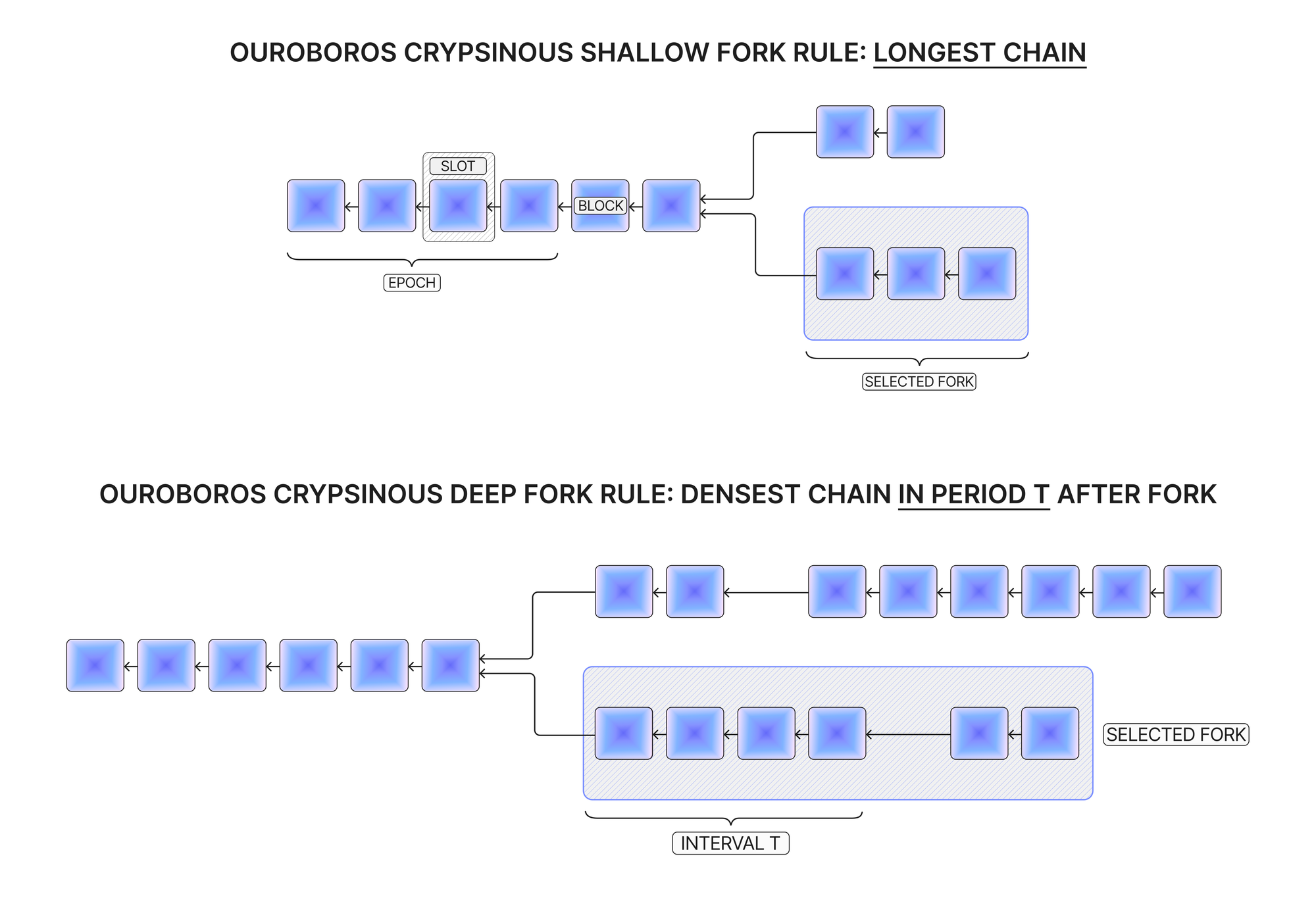
The more distinct features of Ouroboros Crypsinous are explained in the following subsections.
Coins and Transactions
Public blockchain ledgers like those used by Bitcoin or Ouroboros Genesis maintain records of transactions which trace the transferred currency units back to when they were mined or minted. Such ledgers have been shown to leak a lot of information, despite relying on pseudonymous addresses. For a true privacy-preserving blockchain, hiding both the parties to a transaction, as well as the value transferred, is critical.
Crypsinous, inspired by Zerocash, preserves privacy by representing value in the form of individual coins, that can be created and spent once. The protocol maintains separate sets representing coins that have been created and can be spent, and those that have already been spent. When a coin is spent, new coins belonging to the recipient are created, resulting in value being transferred without leaking information about the transfer.
The way this works is that every participant in the protocol has a secret key for sending coins and a corresponding public key. When a new coin is created, a commitment to its value, the owner’s public key, and a random value called a “nonce” are added to a protocol-wide Merkle tree of coins usable for spending, \(\mathbb{C}^{spend}\). To transfer value, the sender uses their secret key to spend at most two coins, and the recipient’s public key is used to create at most two new coins belonging to the recipient. When a coin is spent, the sender reveals its serial number - derived from their secret key and the coin’s nonce - and adds it to the set of serial numbers of spent coins, \(\mathbb{S}\). It is important to note that a coin’s commitment and serial number cannot be linked to each other, further preserving privacy.
A transfer transaction includes a zero knowledge proof that:
- The sender owns the coin(s) being spent. This is proven by showing that the sender knows the private key corresponding to the public key used to create the coin.
- The commitment(s) of the coin(s) being spent are in \(\mathbb{C}^{spend}\)
- The created coin(s) will have the same combined value as that of the coin(s) being spent
- Some other consistency properties
When the serial number of a coin is revealed, validators can verify that this serial number is not in \(\mathbb{S}\). The coin details necessary for spending are sent to the recipient in an encrypted cyphertext. Because the validity of a transfer transaction is proven in zero knowledge, and only the coin commitments and serial numbers are publicly stored rather than the sender and recipient keys directly, the transaction’s parties and transferred value remain private to third parties.
Keys
In the previous section, we briefly mentioned the public and secret keys used to send and receive coins, as well as an encryption scheme for sensitive values sent along with the transfer. These represent distinct key pairs - one pair used by parties for transactions, and another for encrypting messages.
Coin Keys
Coin keys are used to spend and create coins in transfer transactions, and are also a critical component of the leadership proofs (see below). Unlike the key pairs used in Zerocash, where the secret key is a random string and the public key is its hash, Crypsinous coin keys are generated in a more complex way in order to be resilient against adaptive corruption. In a nutshell, even if an adversary gains access to an honest party’s secret key, they cannot use it to create proofs referring to past slots.
This property, known as forward security, is especially important for Crypsinous’ leadership proofs. Without it, adversaries who can corrupt enough honest parties would be able to generate competing forks due to their ability to generate proofs of leadership for slots in the past. Unlike in PoW chains, where creating a fork requires a major investment of computing resources to re-mine the forked blocks, the cost of creating a fork on a chain with no forward security is minimal.
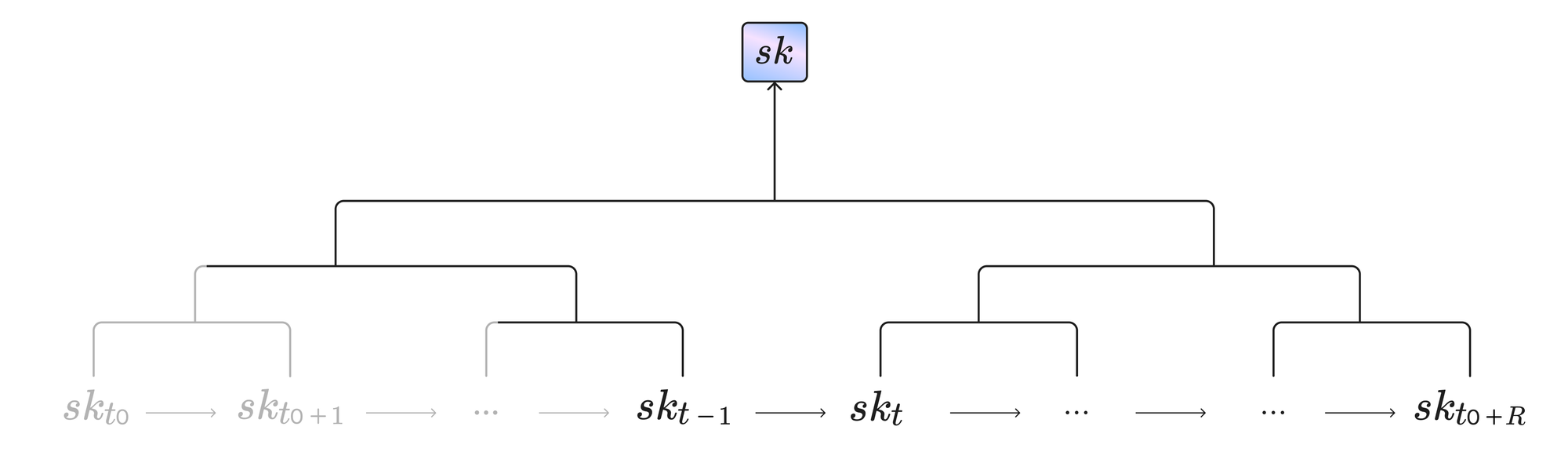
Forward security emerges in Crypsinous due to a process known as key erasure. Instead of a random string, a coin secret key is formed by the following steps:
- Generate a random string for the initial slot \(t_0\), known as \(sk_{t_0}\)
- Deterministically derive \(sk_{t_0+1}\) from \(sk_{t_0}\), and \(sk_{t_0+2}\) from \(sk_{t_0+1}\), etc… continuing until \(sk_{t_0+R}\) for a large bound \(R\)
- Create a Merkle tree over all the elements from the first two steps
The root of this Merkle tree is used as the coin secret key \(sk\), and the hash of this root becomes the coin public key \(pk\). After the time \(R\) passes, the secret key and its tree can be refreshed by the user.
Key erasure works by having honest nodes destroy the leaves of this tree after the corresponding slot has passed. Preventing adversaries from retroactively using a secret key from a corrupted honest party is as simple as requiring them to prove that they know the Merkle path of the \(sk_t\) at their desired slot \(t\) in the past. Because the honest party will have erased that part of the tree, the adversary cannot produce the required Merkle path to create proofs for that time. This whole construction is demonstrated in the following diagram:
It is important to note that each coin can have its own distinct key pair, rather than each party only using one such pair. This is not a problem for the security analysis, since parties are able to adopt any number of alternative identities in permissionless settings.
Encryption Keys
Users also maintain key pairs used for encrypting transaction information. Just like coin keys, encryption keys must also be forward secure, but traditional forward-secure encryption schemes leak information about the transaction recipient. Therefore, Crypsinous uses key-private forward secure encryption to prevent recipient public keys from being publicised.
Unfortunately, using such a scheme makes Crypsinous secure only against adaptive adversaries. This security assumption is technically weaker than Ouroboros Genesis’ security against fully-adaptive adversaries (who can corrupt participants immediately), but has been deemed sufficient for the network environment where messages are subject to a delivery delay. Since a recipient’s private key is updated with every decryption, an adversary that attempts to corrupt it at a time \(\tau\) will only have access to its “delayed” updated key at time \(\tau+\Delta\).
This type of forward secure encryption is what enables Crypsinous to maintain its private ledger. Because only transaction senders and their intended recipients can decrypt the transaction details - and even then, only the details that the decrypting party is permitted to see - the ledger is perceived as a “black box” by other parties. Even in the situation where information is leaked due to an honest party being compromised, the private ledger still reveals less information than a standard ledger would.
Leadership Election
In Ouroboros Praos and Genesis, each participant locally determines whether they are a block leader by running a random function on the epoch randomness and slot number. If the result is less than a threshold value that depends on their relative stake, that participant is a block leader for that slot. In Ouroboros Crypsinous, however, this scheme cannot be used since it reveals information about a participant’s stake. Instead, the authors present a solution to maintain privacy without doing away with Praos’ local leadership election mechanism.
Crypsinous coins, in addition to functioning as representations of value in transfer transactions, are also considered separately for leadership election. Therefore, the protocol maintains a Merkle tree \(\mathbb{C}^{lead}\) of coin commitments eligible for leadership separately from the tree of coin commitments eligible for spending \(\mathbb{C}^{spend}\) and the set of serial numbers of spent coins \(\mathbb{S}\).
Epoch Randomness
Just like Praos and Genesis, Crypsinous generates a new source of randomness at the beginning of each epoch. This randomness, denoted \(\eta_{e_j}\) for the epoch \(e_j\), is sampled via a maliciously unpredictable pseudorandom function (MUPRF) based on:
- The previous epoch randomness \(\eta_{e_{j-1}}\)
- The epoch number \(j\)
- And the randomness contributions \(\rho_i\) associated with the first two thirds of blocks in the previous epoch (see below)
MUPRFs are used here, as well as for other applications in Crypsinous where deterministic but unpredictable output is required, in order to prevent adversaries from using “bad keys” to predict an output to such a function.
Leadership Eligibility
In Crypsinous, leadership elections are run by participants for each coin separately, as opposed to by each party as in Praos. First, the participant must ensure that the coin being considered for leadership is actually eligible to be a block leader - that is, its commitment is in \(\mathbb{C}^{lead}\) and the coin was not spent. If the coin is eligible, the participant runs the leadership election by evaluating a MUPRF on the string formed by concatenating:
- The constant “LEAD”,
- The epoch randomness \(\eta_{e_j}\),
- And the slot number \(s\)
Unlike in Praos, where verifiable random functions are used to ensure that the output is generated correctly, the verification of this MUPRF output occurs as part of the associated zero knowledge proof. This function, which is seeded with a concatenation of the coin’s secret key and the coin’s nonce, produces an output that is then compared to the coin’s threshold value \(T_c\) for that epoch. If this output is less than \(T_c\), the coin is eligible to be a block leader for that slot.
The threshold value \(T_c\) used for the leadership election is calculated using the same function used by Praos, with its input being the coin’s stake relative to the total stake. Since the other parties’ stakes are private in Crypsinous, the total stake must be estimated in some way. The Crypsinous paper does not provide a mechanism for total stake estimation, which is a notable omission that will be discussed in detail in a future article. In any case, \(T_c\) is calculated in such a way that the likelihood of any of a Crypsinous participant’s coins winning the leadership election for a slot is around same as the likelihood for a Genesis participant to win the election. The only difference emerges when a Crypsinous coin is created within the epoch and is therefore ineligible for leadership, reducing its owner’s chances of winning.
Proof of Leadership
In order to extend the blockchain with an additional block, a participant must include a proof of leadership (PoL) that indicates that their coin won the leadership election for the relevant slot. They submit a leadership transaction, with a zero knowledge proof that:
- The block leader owns the winning coin. This is proven by showing that the sender knows the private key corresponding to the public key used to create the coin.
- The winning coin’s commitment is in \(\mathbb{C}^{lead}\)
- The MUPRF output of the winning coin is less than the required threshold
- The block leader knows a Merkle path in the secret key tree to the leaf for the correct slot time. This prevents adversaries from creating proofs of leadership for past slots (see above, “Coin Keys”).
- Some other consistency properties
Just like for transfer transactions, validators will check the revealed serial number to ensure that it is not in \(\mathbb{S}\). Because the winning coin’s serial number is revealed to prove that it has not been spent, the coin is evolved into a new coin with the same value once the leadership proof is submitted. This is done by updating the coin’s nonce via a pseudorandom function and deleting the old nonce, allowing the new coin to be eligible both for spending and for future leadership. Since this nonce update is deterministic, adaptive adversaries cannot “grind” the outputs until they create an evolved coin that wins an election. Once a coin is spent and a corresponding new coin is created for the recipient, the new coin is not eligible for leadership for the remainder of that epoch.
In addition to the broadcast of a new chain with the appended block, the block leader will broadcast the leadership transaction separately. This ensures that the evolved coin will be accepted as valid, even if the consensus does not adopt the new chain.
As part of the leadership transaction, the leader includes a randomness contribution \(\rho\) which is used to calculate the randomness for the subsequent epoch. \(\rho\) is calculated by evaluating a MUPRF seeded by the coin secret key on the string formed by concatenating:
- The constant “NONCE”,
- The epoch randomness \(\eta_{e_j}\),
- And the slot number \(s\)
In the next article in this series, we will discuss some problems with Crypsinous and introduce Cryptarchia, an improvement designed by the Nomos team.

