Consensus

The Ouroboros Family of Consensus Protocols: Ouroboros, Praos, Genesis

In this article, we will discuss the original Ouroboros protocol, as well as its descendants Praos and Genesis.

Nomos Team

Jan 17, 2025 • 11 min read

Part 1 of a series on the Ouroboros Family of Consensus Protocols

In recent years, Proof of Stake (PoS) consensus mechanisms have become a popular choice for modern blockchains and are widely seen as the most viable alternative to Proof of Work (PoW). The most notable example of this is Ethereum, which switched from PoW to PoS in 2022. The main reasons to use PoS over PoW is its much lower energy consumption, and consequently lower barrier to entry for participants with limited computing resources.

The Ouroboros consensus protocol was introduced in 2017 as the first provably secure Proof of Stake system, leading to the rise of several iterations collectively referred to as the “Ouroboros family”. Several of these protocols have been used by the Cardano blockchain and other blockchain networks. Of particular interest to the Nomos project is Ouroboros Crypsinous, which introduces privacy-preserving properties to the Ouroboros model.

This blog series will give an overview of the development of this family of protocols. In this first instalment, we will discuss the original Ouroboros protocol, as well as its non-privacy-focused descendants Ouroboros Praos and Ouroboros Genesis.

Background

Blockchain Basics

The basic goal of a consensus protocol is to enable a group of parties to agree on a blockchain - a type of distributed, dynamic ledger of transactions. The two main properties of such a ledger are:

Liveness: An honest transaction will be included in the ledger without undue delay.
Persistence: Once a transaction is in the ledger for some time, it cannot be changed or removed.

In this decentralised environment, there may be some parties (known as adversaries) that act dishonestly in order to disrupt the system. Therefore, a consensus protocol must also provide a way to prevent adversaries from violating either of the above properties. For our purposes, adversaries are assumed to possess a minority of the total computational power (PoW) or economic stake (PoS).

Proof of Work

PoW blockchain protocols such as Bitcoin group transactions together into blocks, appending blocks to each other to grow the blockchain. Each block also includes a hash of the previous block and a nonce. Bitcoin miners test different nonce values to attempt to obtain a hash of the block that is lower than the network’s target value. If a miner succeeds, they can append their new block to the chain and broadcast it.

Because any adversary has less computational power than the combination of all the honest participants, it is infeasible for them to build an alternative blockchain that is longer than the honest chain. Therefore, the longest blockchain available at any given moment can be assumed by participants to be the honest chain. This is known as the fork choice rule.

Proof of Stake

A major problem with this PoW protocol is the energy consumption required to mine new blocks, which in Bitcoin’s case is about 176 TWh of electricity each year - equivalent to the power consumption of Poland at the time of writing. Proof of Stake, by contrast, selects one party at random to build the next block, with the probability of being elected block leader determined by how many crypto-assets that party has staked, as a proportion of the total. Essentially, a unit of currency is randomly selected, and its owner becomes the leader for the next block. PoS therefore relies on the economic difficulty of amassing the majority of staked crypto-assets rather than the computational difficulty of controlling the majority of the computing power, as in PoW.

Ouroboros Classic

The first iteration of Ouroboros, retroactively referred to as Ouroboros Classic, was introduced in a 2017 paper. Unlike some other PoS protocols, the Ouroboros Classic paper provides a formal proof that the protocol will maintain its persistence and liveness under the following conditions:

Honest participants hold a majority of the staked crypto-assets
All honest participants communicate synchronously with all other participants
Most participants selected for generating randomness (see below) are available to do so
Participants do not remain offline for prolonged periods of time
Adversaries may send arbitrary messages to arbitrary participants, with arbitrary delays

To achieve synchronicity, time in Ouroboros Classic is divided into discrete units called slots, each of which is longer than any expected communication delay on the network. The current slot number is known to every participant and any message sent at the beginning of a slot will be received by the end of the slot. Every slot has a different block leader and the potential to add at most one new block to the chain, signed by this block leader.

In turn, slots are grouped into larger periods of time known as epochs. While slots are the atomic units of time for appending blocks and communication between participants, epochs are the time periods used for determining the schedule of slot leaders for the slots in the following epoch.

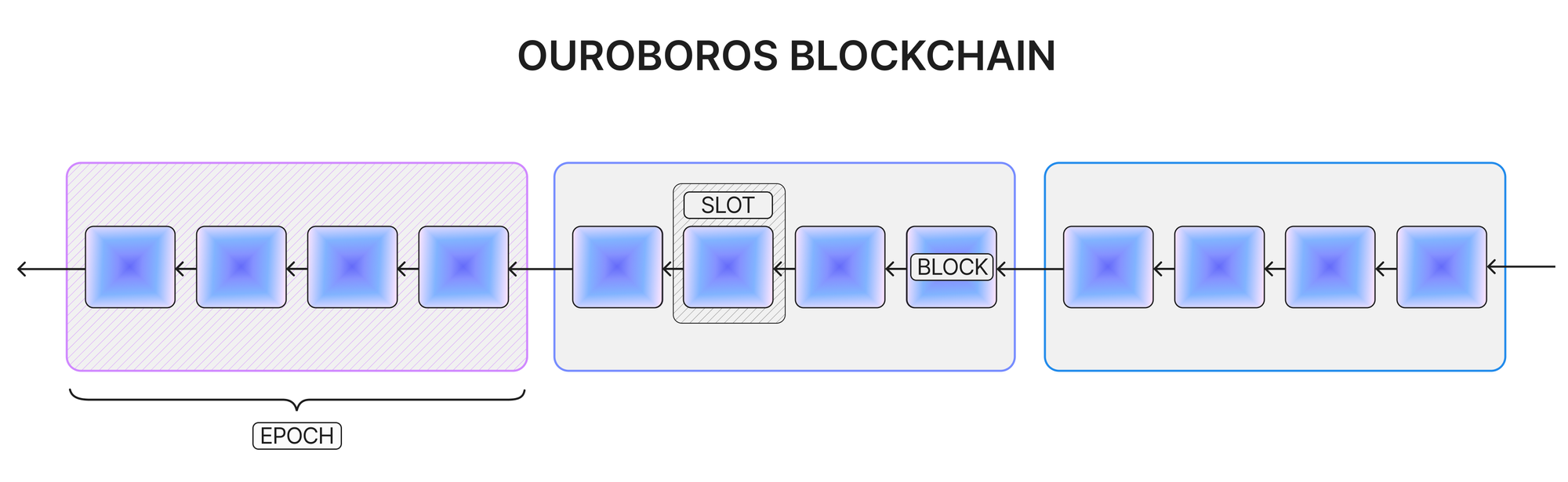
Public Leadership Election via PVSS

Ensuring that the randomness used in the leadership election process cannot be biased by an adversary is one of the key challenges of designing a PoS system. Ouroboros Classic uses a multi-party computation scheme known as Publicly Verifiable Secret Sharing (PVSS) to generate an unbiased random seed every epoch. PVSS schemes are used to split a secret value in such a way that only an honest majority of parties can recover the secret. They also allow third parties to verify that the shares are valid without learning the shares themselves. Using PVSS enables Ouroboros Classic to generate clean randomness with input from several parties, with a guaranteed output so long as there is an honest majority of participants. More information on the PVSS scheme used in Ouroboros Classic can be found in this paper.

During each epoch, the set of block leaders \(\{U_1, ..., U_R\}\) for that epoch’s \(R\) slots engage in PVSS to generate the randomness used in the following epoch. Each leader \(U_i\) generates a random secret key \(s_i\) as well as an associated public key \(y_i\), which is posted on chain. Every honest \(U_i\) then uses PVSS to split their secret \(s_i\) into \(R\) shares, where each share \(\beta_i\) is encrypted with the associated leader’s public key \(y_i\). These encrypted shares are also posted on chain, in what is known as the commitment phase.

Closer to the end of the epoch, the leadership election process enters the reveal phase. Each leader \(U_i\) uses their private key \(s_i\) to decrypt shares of the other parties’ secrets that were encrypted with its public key. Of course, only shares that can be verified to have been generated correctly are decrypted. These revealed secrets, \(\sigma_1,...,\sigma_R\), are then posted on chain.

To generate the randomness for the next epoch, any party (including third parties) can reconstruct the secrets \(s_i\) created by the majority of leaders. These secrets are hashed and XOR’d together to produce the necessary randomness. At this point, the protocol takes a snapshot of the asset distribution. Based on this distribution, the randomness is used as a seed to a pseudorandom function used to select several crypto-asset units, corresponding to the number of slots in the next epoch. The owners of these units become the block leaders in the next epoch.

Longest Chain Fork Choice Rule

Just like in Bitcoin, honest Ouroboros Classic participants select the longest available chain at any given moment to be the honest chain. However, constructing an adversarial longest chain is no longer computationally difficult to do, since an adversary can generate any number of blocks with slot numbers corresponding to those where they are the leader.

Despite these limitations, the authors of the Ouroboros Classic paper prove that deep adversarial forks are very rare, assuming a binomial distribution of leader schedules and the synchronous setting described at the beginning of this section. In fact, the probability of the longest chain and second-longest chain diverging in the most recent \(k\) slots decreases exponentially as \(k\) increases. This quality is known as the common prefix property, and is essential for ensuring a blockchain’s persistence.

Liveness, on the other hand, follows from the chain growth and chain quality properties. Chain growth - that the chain adopted by an honest party increases over \(k\) slots by at least the set fraction \(\tau k\) - follows from the fact that honest leaders will always add a new block to the longest chain. Chain quality - that one of the last \(k\) blocks was generated honestly - is proven in the paper to be reducible to a claim about the common prefix.

As it turns out, these three properties together prove that the longest chain rule in Ouroboros Classic still works to guarantee persistence and liveness in nearly all scenarios.

Ouroboros Praos

Ouroboros Praos, introduced in a 2018 paper by many of the same authors who worked on Ouroboros Classic, was intended as an improvement on the latter protocol. Ouroboros Praos extends the security guarantees of Ouroboros Classic into a semi-synchronous setting with more powerful adversaries that can corrupt any participant immediately. More specifically, Ouroboros Praos has been proven to maintain its persistence and liveness under the following conditions:

Honest participants hold a majority of the staked crypto-assets
Honest participants’ communication may be subject to a significant delay
Adversaries have full control over the delays involved when sending arbitrary messages to arbitrary participants
These delays are not known to the protocol

These new conditions, which allow for significant communication delays of up to several slots that are not known to honest participants, are referred to as the semi-synchronous setting. As in Ouroboros Classic, time in Ouroboros Praos is divided into slots and epochs, and the longest chain is selected by the fork choice rule. However, each participant now decides locally whether they are the block leader by running a verifiable private test, rather engaging in a public leadership election as in Ouroboros Classic.

Private Leadership Election via VRFs

The most important change introduced in Ouroboros Praos is its local determination of block leadership. For every slot, each participant runs a Verifiable Random Function (VRF) to determine whether they are the block leader. A VRF is a type of function that uses a provided input to produce a pseudorandom output, together with a proof. This proof can be used to verify that a given input was used to produce a given output, but the output cannot be inferred from the input or vice versa. The VRF used by Ouroboros Praos participants is a stronger type of VRF that produces unpredictable outputs even if an adversary can maliciously create their own keys.

With private leadership elections, parties do not know whether another party is a block leader until they receive a valid block signed by that party. This property ensures that adversaries cannot target future block leaders, which is a significant weakness of Ouroboros Classic’s public leadership schedule. A consequence of this type of election is that a slot may have zero, one, or multiple honest block leaders. However, the authors of the Ouroboros Praos paper prove that blockchains generated according to these dynamics retain their critical properties of persistence and liveness. In fact, the presence of slots without any block leaders gives honest participants extra time to synchronise.

At the beginning of each epoch, every participant generates the new nonce that will be used as a source of randomness for the VRF in the current epoch. This is done by concatenating the following information:

The previous nonce \(\eta_{j-1}\),
The epoch number \(j\),
And the random VRF outputs \(y_1,...,y_n\) associated with the first two thirds of blocks in the previous epoch (see below).

This value is then hashed to produce the nonce \(\eta_j\) for the upcoming epoch. A snapshot is taken by the protocol of the stake distribution at the beginning of each epoch, with threshold values \(T_i^{j+1}\) assigned to every stakeholder \(U_i\) based on their relative stake in the epoch \(e_j\). Every \(U_i\) will use their threshold value generated in \(e_j\) to decide whether they will be a block leader in the following epoch \(e_{j+1}\).

In each slot, every participant \(U_i\) runs the VRF, keyed with their secret key, on the input formed by concatenating:

The epoch nonce \(\eta_j\),
The slot number \(s\),
And the constant “TEST”.

If the output produced by the VRF is greater than or equal to the threshold value \(T_i^j\) associated with \(U_i\) from the previous epoch \(e_{j-1}\), then \(U_i\) is not the leader for slot \(s\). If it is the leader for that slot, \(U_i\) will run the VRF again on the same input as above, only replacing “TEST” with “NONCE” to provide domain separation. When it builds the next block, \(U_i\) will include the two VRF outputs and proofs together with the transaction data and a signature. The proof generated from the input with “TEST” allows anybody to verify whether \(U_i\) was a valid block leader for that slot, whereas the proof generated from the input with “NONCE” is used to generate the random nonce for the next epoch.

Resisting Corruption with Key Evolving Signatures

Another change in Ouroboros Praos is the use of key evolving signatures by block leaders to sign blocks they create. A key evolving signature scheme allows the private key used by the signer to be updated, while still remaining verifiable with the same public key. In Ouroboros Praos, honest participants generate new private keys at regular time intervals and discard their old private keys. This ensures that an adversary that corrupts an honest party cannot sign blocks for past slots by using that party’s private key. Since the private keys keep evolving and old keys are discarded, any party can verify whether a block was signed at a particular point in time.

Ouroboros Genesis

Ouroboros Genesis was introduced in a 2018 paper by many of the same authors who worked on Ouroboros Praos and Ouroboros Classic, and is currently used by Cardano. Ouroboros Genesis extends the security of Ouroboros Praos to include situations where any number of parties may not be fully operational, due to real-world scenarios such as network problems or OS updates. This is referred to in the paper as the dynamic availability setting. Whereas Ouroboros Praos improved Ouroboros Classic’s leadership election process while leaving the fork choice rule basically unchanged, Ouroboros Genesis introduces a novel fork choice rule without changing Ouroboros Praos’ private leadership election process.

A Novel Fork Choice Rule

The longest chain fork choice rule in PoW protocols like Bitcoin ensures that a participant joining or rejoining the protocol can safely assume that the longest chain is the honest one, since it was built with more computational resources than any alternative chain. In PoS blockchains, however, the longest chain rule only ensures that adversarial chains are not chosen if honest parties invoke the rule fairly frequently. If a participant joins or rejoins after a prolonged absence, they have no trustless way of knowing if the longest chain they see is actually the honest one.

A major problem with Ouroboros Classic and Ouroboros Praos in the dynamic availability setting is that parties who join the consensus protocol (or re-join after a prolonged absence) must be given an initial honest blockchain from a trusted party, in a process known as “checkpointing”. The fork choice rule used in Ouroboros Genesis allows these parties to bootstrap their blockchain while only relying on the original “genesis” block. In essence, this allows any party to validate a blockchain’s entire history without being an active participant in it.

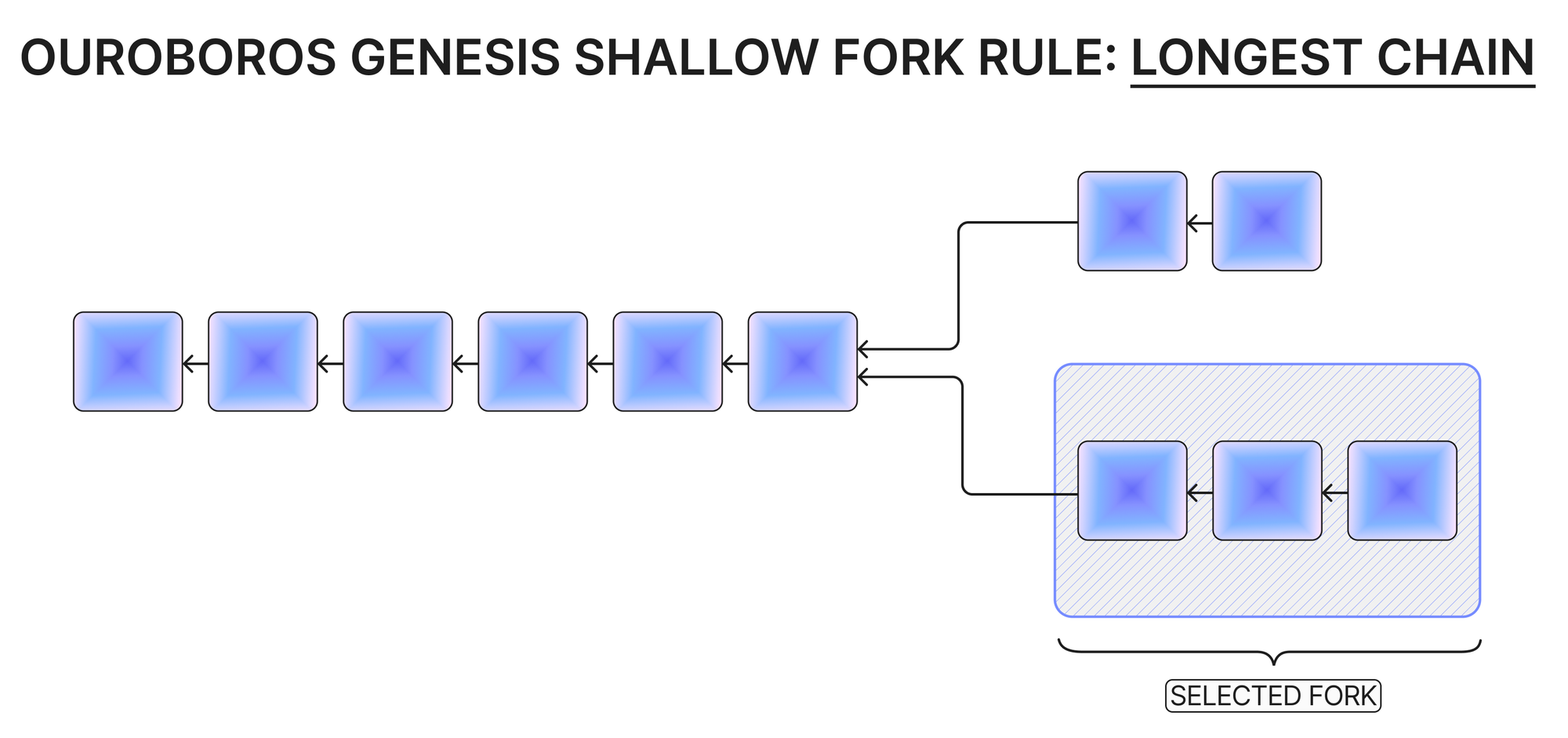
The fork choice rule in Ouroboros Genesis takes a different form depending on how long ago the candidate chain forked away from the participant’s local chain (if they are joining anew, this would just be the genesis block). The two rules are:

If there is a chain that diverges from the local chain by less than \(k\) blocks and this candidate chain is longer than the local chain, adopt that chain.

If there is a chain that diverges from the local chain by more than \(k\) blocks and this candidate chain has more blocks produced over the time period \(T\) immediately after the fork, adopt that chain.

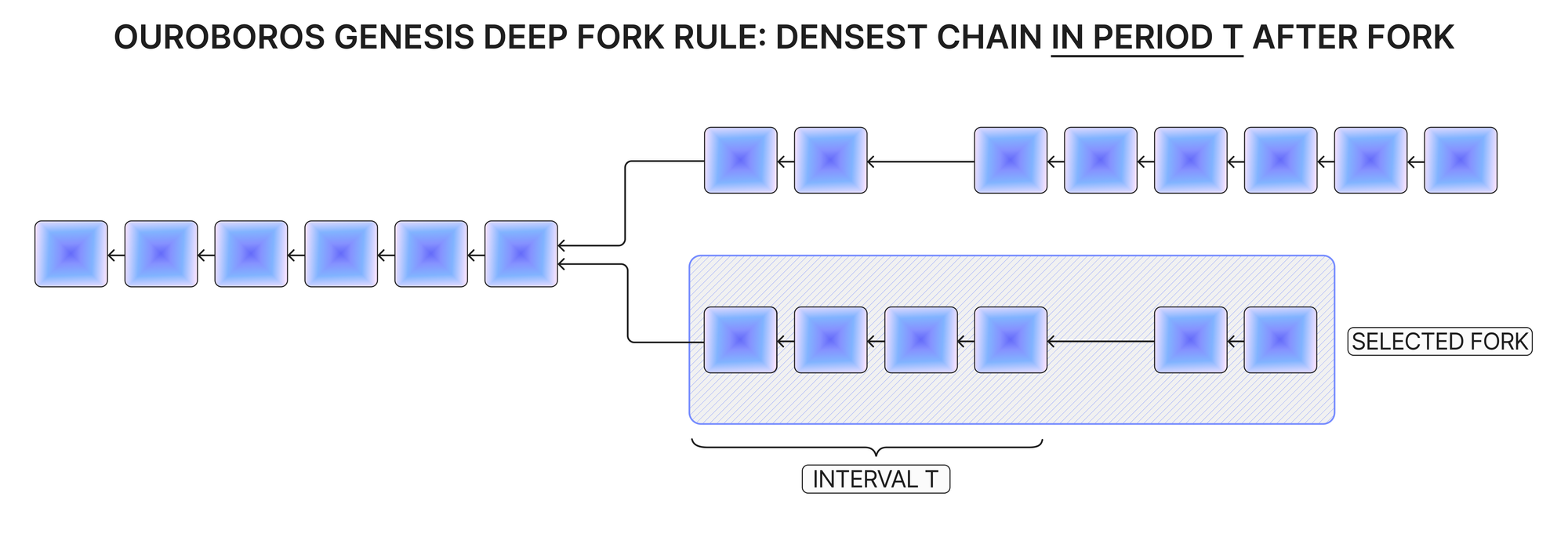
The first rule, for shallow forks, corresponds to the longest chain fork choice rule in Ouroboros Classic and Ouroboros Praos, and the requirement for the fork to be shallow here is in essence equivalent to these previous protocols’ requirements for participants not to be offline for too long. The second rule is based on the property, proven in the Ouroboros Genesis paper, that any adversarial fork will exhibit a lower block density than the honest chain in the period immediately after the last common block. The intuition behind this rule is that the densest chain over the initial period after the fork was the longest chain at that point in time, and therefore would have been adopted as the honest chain if the participant had been actively monitoring the blockchain.

In the next article in this series, we will discuss Ouroboros Crypsinous and its descendant Cryptarchia, designed by the Nomos team.

Sources and Further Reading