Preventing Wealth Concentration in PoS Systems: The Role of Stake Relativisation

The recent transition of DarkFi from the PoS-based Ouroboros Crypsinous protocol due to wealth concentration findings motivated us to investigate the matter. We found that wealth concentration does not emerge from a PoS system driven by Crypsinous leader election function if certain conditions are met.
In our previous article, we shared findings on the impact of VRFs on wealth concentration in the Cryptsinous leader election function. By favouring either the lowest or highest Verifiable Random Function (VRF) output or a stochastic approach, we demonstrate how these rules can mitigate or exacerbate wealth disparities among validators.
In this research, we first focus on the impact of stake relativisation in the Crypsinous leader election function under conditions where the total stake in the protocol is unknown to the protocol itself, which is a more realistic assumption. We explore how an algorithm that learns about the stake impacts wealth concentration within a PoS system. Secondly, we explore strategies to address the challenges posed by defining Crypsinous' leadership election function in terms of relative stake.
Defining Crypsinous' Relative Stake
The Crypsinous leadership lottery function is defined in terms of relative stake. The function differentiates between "old coins" and "young coins," impacting their eligibility for participation in leadership proofs.
There are two possible interpretations of the relative stake defined by Crypsinous: one based on the total supply of coins and another based on the total number of old coins. We focus on the latter interpretation, aiming to estimate the total number of old coins to represent the total stake.
Defining Total Stake
We introduce a methodology to adjust the initial estimate of total stake across epochs based on the observed results of leadership elections. This adjustment is governed by parameters such as the learning rate and epoch length to refine the estimate and reflect the network's total stake more accurately. We observe this in the following equation:
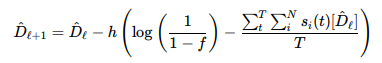
In our study, we further elaborate on how to select parameters h and T to balance three critical factors:
- Accuracy - how close the estimate is to the actual total stake.
- Stability - how stable the estimate is over time, particularly at the fixed point where it is supposed to converge.
- Convergence speed - how fast the estimate approaches the actual value of the total stake.
Mathematically, we show how the parameters ensure that the estimate converges to a stable value that accurately reflects the total stake within an acceptable time frame.
Stake Relativization: Algorithmic Learning
Cryptarchia, our improvement on Crypsinous, operates on the premise that the total stake in the protocol is unknown to the protocol itself. Instead, it utilises an algorithmic approach to approximate or ‘learn’ the total stake, a crucial factor for the protocol's leader election function. We conduct simulations to explore the effects of stake relativisation on wealth concentration.
Simulation Parameters
Table 1: Parameters for base case simulation
*Pareto distribution with shape 15; initial guess of the staked supply: 10%, 25%, 50%, 75%, 100%; rewards per epoch: 10%, 20%, or 30% of the initial circulating supply, divided by the number of epochs.
Our simulations were run on a GPU architecture, mimicking Cardano’s parameters and allowing us to test many variables and interactions.
Simulations: Stochastic Fork-Choice Rule
The stochastic fork-choice rule gives each selected block producer an equal chance of being chosen as a block leader, regardless of their stake size.
Following the base case parameters, we investigate the following scenario:
- The supply increases by 30% throughout the simulation
- The initial guess about the stake supply equals the initial circulating supply.
The consistency of results suggests that these factors—rewards per epoch and the estimated staked supply—do not significantly impact the distribution of wealth among validators in this context.
Figure 1: Stochastic Fork-Choice Rule Simulations
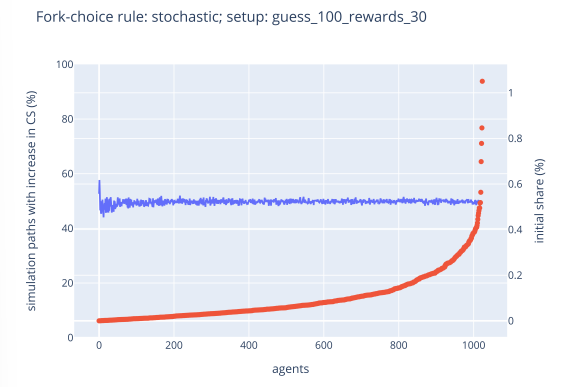
We also show the graphic results on wealth concentration outcomes across the spectrum of validator wealth, focusing on the bottom 20, mid-20, and top 10 validators. Our research paper provides detailed results.
Sensitivity Analysis: VRF Fork-Choice Rule
Through a series of simulations, we analysed how the lowest VRF fork-choice rule influences the stake dynamics over time across different segments of validators, categorised by their initial stake sizes.
We do not analyse the highest fork-choice rule as our previous research has already proven that it leads to undesired consequences.
Figure 2: Sensitivity Analysis - Lowest VRF Fork-Choice Rule
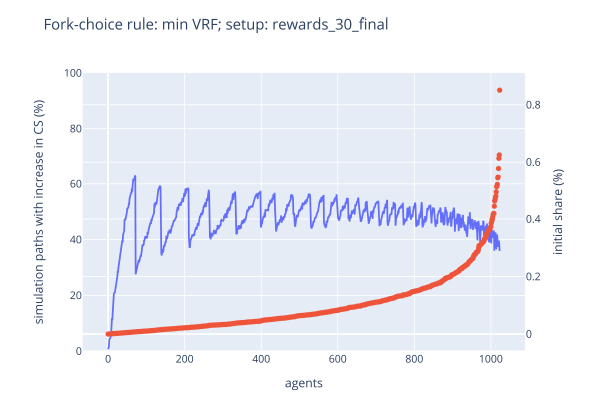
We will soon share our research paper for more detailed results across different validators.
Concluding Remarks
This research contributes to understanding how PoS systems can be designed or modified to prevent wealth concentration and ensure a more equitable distribution of rewards and influence among participants.
Through detailed computational analysis, we explored the role of stake relativisation in preventing wealth concentration in Ouroboros Crypsinous. We also propose modifications to the new epoch protocol and leadership proofs for the protocol to offer a more fair election system.
Research like this contributes to the ecosystem by providing practical solutions for addressing the limitations of specific protocols. Additionally, it offers enhanced insight into the system's dynamics, enabling a deeper understanding and fostering trust among users. With established trust, comprehensive knowledge, and robust foundations, these protocols can be leveraged for various applications.

