Lottery Difficulty in Private PoS: The Case of Cryptarchia
Learn how Nomos adjusts the consensus lottery difficulty based on network activity.

In Proof of Stake (PoS) consensus protocols, the likelihood of an eligible participant being chosen as a block proposer (the same entity as the leader in many protocols) is known as the lottery difficulty. This difficulty depends on their relative stake - that is, the participant’s stake divided by the total eligible (or active) stake held by all participants. This poses a problem for privacy-preserving PoS protocols, since their privacy properties ensure that the total active stake in the network cannot be directly observed. Without this information, it is difficult to accurately calculate relative stake, complicating the lottery difficulty adjustment process required to maintain a stable block production rate.
In Cryptarchia, Nomos’ Private Proof of Stake (PPoS) consensus protocol, this problem is solved by having the leadership lottery estimate the total active stake based on the observed activity of the network. This article will introduce and explain this component of the Cryptarchia leadership lottery, known as the total stake inference algorithm. It will also touch upon the motivations for its design, as well as some other proposed solutions.
Problem: How Can Stake be Private in PoS?
There is an inherent tension between design objectives that must be resolved when creating a PoS system that preserves proposer privacy. On the one hand, privacy demands that the stake of each consensus participant remain hidden from others. On the other, knowing the sum total of these stake amounts is necessary for calculating each participant’s relative stake, and therefore their lottery difficulty. While a solution to this problem is far from straightforward, the paper describing Crypsinous (the PPoS protocol that inspired Cryptarchia) does not include a method for inferring total active stake. This left the issue open for the Nomos team to solve.
It may be tempting to simply use the total supply of all tokens that exist in the network for the denominator when calculating relative stake, rather than the total active stake consisting only of tokens eligible for consensus. However, this approach introduces a bias by underestimating relative stake as a result of using the larger total supply value in its denominator. This increases the lottery difficulty, reducing the block production rate and makes it fall well below the target rate. In addition, as the proportion of active stake to total supply is expected to change over time, the fluctuating bias will result in uncertain block finality times. It was therefore necessary to find a way of estimating the total active stake to ensure that Cryptarchia functions as expected.
DarkFi, a privacy-preserving blockchain, made an attempt at implementing Crypsinous and came up with their own solution to this problem. Their team decided to use a PID mechanism to control the block production rate, adjusting it periodically to ensure that a proposer would be chosen almost every time the lottery is run. Besides for the fact that correctly modelling a system to ensure that the PID operates correctly is difficult, this approach fundamentally undermines the security of consensus protocols like Cryptarchia and Crypsinous. This is because protocols of this kind rely on a stable block production rate and long breaks between blocks to ensure that blocks can be disseminated across the network. In any case, DarkFi chose to move away from using Crypsinous for consensus in favour of PoW mining algorithm RandomX due to concerns about wealth concentration in Proof of Stake. These concerns have been addressed previously on this blog.
Cryptarchia Total Stake Inference
Cryptarchia’s Leadership Lottery
In Cryptarchia, time is divided into small discrete units known as slots that are grouped together into longer periods called epochs. In every epoch, proposer(s) are selected by running random lotteries for every slot of the following epoch. These leadership lotteries are run locally by every eligible participant. Essentially, each lottery involves participants comparing the output of a pseudorandom function to a threshold value that depends on the participant’s relative stake (which remains private). If this output is less than the threshold, the participant is considered to have won the proposal (or leadership) rights for the slot under consideration. Therefore, a greater relative stake corresponds to a greater likelihood of winning the lottery, and vice versa. The lottery process in Cryptarchia is intended to produce a steady 1/30th of slots that have new proposals, known as occupied slots.
More information about Cryptarchia’s leadership lottery can be found in a previous blog post. Note that the total stake inference algorithm described there is outdated, and has been replaced by the algorithm described in this article.
Intuition for Lottery Difficulty Adjustment
Cryptarchia’s total stake inference algorithm is based on the insight that a rise in the block production rate indicates that more stake is participating in consensus than expected, and the opposite is true when the rate decreases. To better understand why this is so, it may be helpful to describe the analogous situation in Bitcoin. An observed increase in block production in Bitcoin means there is more hashing power in the network. To maintain a stable block production rate, the mining difficulty must be increased.
Similarly, an increase in block production in Cryptarchia signals an increase in participating stake, and prompts the protocol to increase the lottery difficulty to maintain the target slot occupancy rate. This is accomplished by increasing the total stake estimate, thereby reducing each participant’s relative stake.
The stake inference algorithm builds on this insight by adjusting the previous total stake estimate every epoch based on the difference between the observed slot occupancy rate and the target rate. This produces a new total stake estimate that slowly approaches closer to the true value, providing accuracy without introducing excessive instability. As a result, the lottery difficulty is adjusted to ensure that the block production rate remains stable.
Algorithm
The Cryptarchia total stake inference algorithm can be presented as follows:
$$ D_{ep+1}=D_{ep}- hD_{ep}\left[f-\frac{B^{\text{honest}}_{ep}}{T}\right] $$
The total stake estimate \(D_{ep+1}\) for the epoch \(ep+1\) is a result of adjusting the previous estimate \(D_{ep}\) by the difference between the target slot occupancy rate \(f\) and the growth rate of the honest chain \(\frac{B^{\text{honest}}_{ep}}{T}\) during an observation period \(T\) of slots. This difference is multiplied by a learning rate \(h\) to control how quickly the estimate responds to observed changes, as well as by \(D_{ep}\) to produce an adjustment based on the previous estimate. Finally, this adjustment is subtracted from \(D_{ep}\) to yield the updated estimate.
Previous Attempts
One thing that stands out about the stake inference algorithm is that it compares the target slot occupancy rate to the growth rate of the honest chain, rather than taking into account all created blocks. In truth, a previous attempt at designing the algorithm did include all valid blocks. A problem with this approach is that its accuracy was dependent on the stake distribution, with more centralised distributions resulting in decreased accuracy.
In any case, a protocol improvement to Cryptarchia made it so that information about blocks not on the honest chain is no longer available to all participants. This prompted a redesign of the stake inference algorithm to ensure that it uses only the honest chain’s growth rate. While the new algorithm’s accuracy is independent of the stake distribution, using the honest chain’s growth rate as a proxy for the overall slot occupancy rate introduces a bias to the estimates. This bias is described in more detail in the section below.
Properties
Accuracy
The accuracy of the stake inference algorithm is a measure of the closeness of the mean inferred total stake to the true total stake, as shown in Figure 1 below.
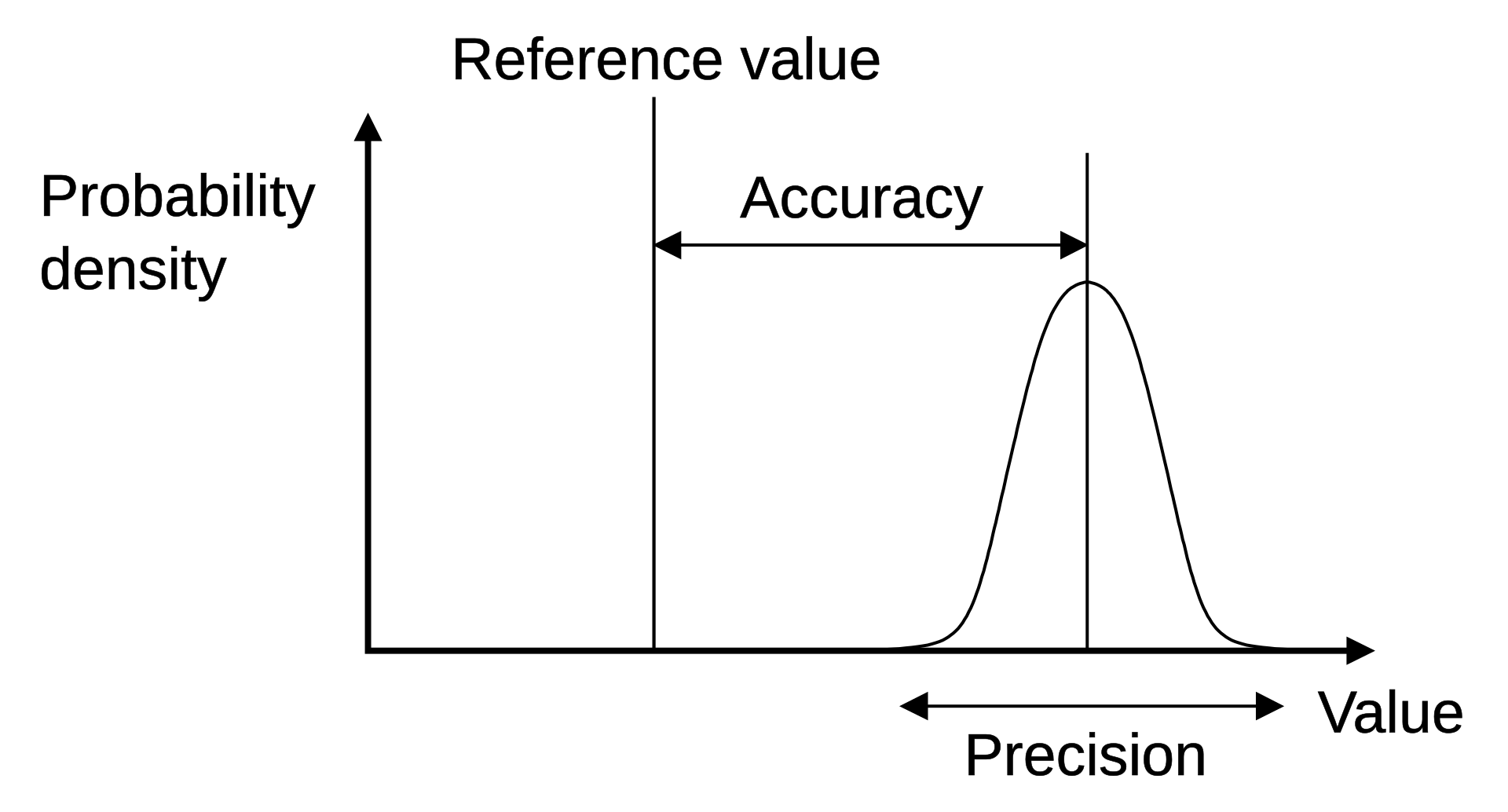
The algorithm described above can be shown to converge to a value fairly close to the true total stake. Under stable conditions, the algorithm will eventually produce values clustered around
$$ \frac{\log(1-f)}{\log(1-f/q)} D_\text{true} $$
where \(D_{\text{true}}\) is the true total stake, \(f\) is the target block production rate, and \(q\) is the proportion of occupied slots that contribute to the honest chain. To put it another way, \({q = \frac{\text{total\_honest\_chain\_slots}}{\text{total\_occupied\_slots}}}\). The distance between this equilibrium estimate and the estimate values during convergence decreases exponentially with every epoch, enabling the algorithm to reach values close to the true total stake in just a few epochs.
It is important to note that the bias \({\frac{\log(1-f)}{\log(1-f/q)}}\) of the inference algorithm is dependent on \(q\), which is also known as the honest slot utilisation rate. This is because, as noted above, the algorithm uses the honest chain’s growth rate as a proxy for the empirical slot occupancy rate. Because Cryptarchia produces more forks with increased network delay, and therefore a lower proportion of blocks on the honest chain, it comes out that a greater network delay will result in a less accurate stake inference value. Based on simulations for the block proposal delay introduced by the Nomos Blend Network, the stake inference algorithm is expected to underestimate the true total stake by about 15% - an acceptable tradeoff given its other properties.
Precision
The precision of the stake inference algorithm is a measure of the degree to which repeated inferences yield similar results at equilibrium, independent of their accuracy. The difference between accuracy and precision is illustrated in Figure 1 above.
Even at equilibrium, the values produced by the total stake inference algorithm will vary somewhat. This variance was determined to be dependent on \(q\), with an increased honest slot utilisation rate resulting in greater variance. Therefore, unlike the accuracy, the precision of inference values actually increases with greater network delays. The Blend Network delays are expected to reduce the variance of the stake inference algorithm by about 40% compared to a hypothetical “perfect network” with all slots used to extend the honest chain.
Stability
Recall that the learning rate \(h\) affects the speed at which the algorithm converges to its new estimate, with greater \(h\) values resulting in a quicker convergence. However, greater learning coefficients introduce more variance, and coefficients above a certain limit produce totally unstable results that never converge. Since the stability bound for \(h\) grows in inverse proportion to \(q\), a lower honest slot utilisation rate will result in greater stability. Just like for precision, an imperfect network provides better stability conditions for the total stake inference algorithm.
Conclusion
Cryptarchia's total stake inference algorithm provides an effective solution to a challenging problem in privacy-preserving PoS systems. By dynamically adjusting the total stake estimate based on the honest chain's growth rate, the algorithm enables accurate relative stake calculations while maintaining stake privacy. As a result, the protocol is able to adjust its leadership lottery difficulty to maintain a stable block production rate. Although the algorithm introduces a small bias in its estimates, this is a reasonable trade-off compared to those of other proposed solutions. Additionally, the Nomos team has identified ways to reduce this bias, which have been left for future versions of the protocol. The chosen approach represents a novel solution to satisfy seemingly contradictory requirements, paving the way for further improvements as Nomos develops.

