Consensus

Nomos’ Cryptarchia: Improving on Ouroboros Crypsinous

Cryptarchia is a PPoS protocol based on Ouroboros Crypsinous, designed specifically for Nomos.

Nomos Team

Feb 21, 2025 • 11 min read

Part 3 of a series on the Ouroboros Family of Consensus Protocols. Read Part 1 here and Part 2 here.

Ouroboros Crypsinous introduced the first formally analysed Private Proof of Stake (PPoS) protocol to the world. Building on a legacy of provably secure consensus protocols known as the Ouroboros family, Crypsinous integrated Zerocash-style private transactions that made it a true alternative to privacy-preserving Proof of Work (PoW) protocols. However, the Crypsinous paper was not completely comprehensive, and left out some crucial details required for any implementation. Additionally, Crypsinous was designed based on cryptography that has become outdated, and has several known issues, including a vulnerability to tagging attacks.

Recognising the advantage of PPoS and the many things that Crypsinous does well prompted the Nomos team to develop an improved protocol, known as Cryptarchia. This new protocol brings the vision behind Crypsinous to life by filling in the gaps in the paper and patching up its issues. Cryptarchia was also designed specifically to provide consensus within Nomos’ modular architecture, and has greater privacy due to Nomos’ anonymous network layer. In this article, we will describe the main differences introduced by Cryptarchia compared to Crypsinous, and the reasons behind the changes. Therefore, this article is best read together with the one describing Crypsinous.

Features Shared by Crypsinous and Cryptarchia

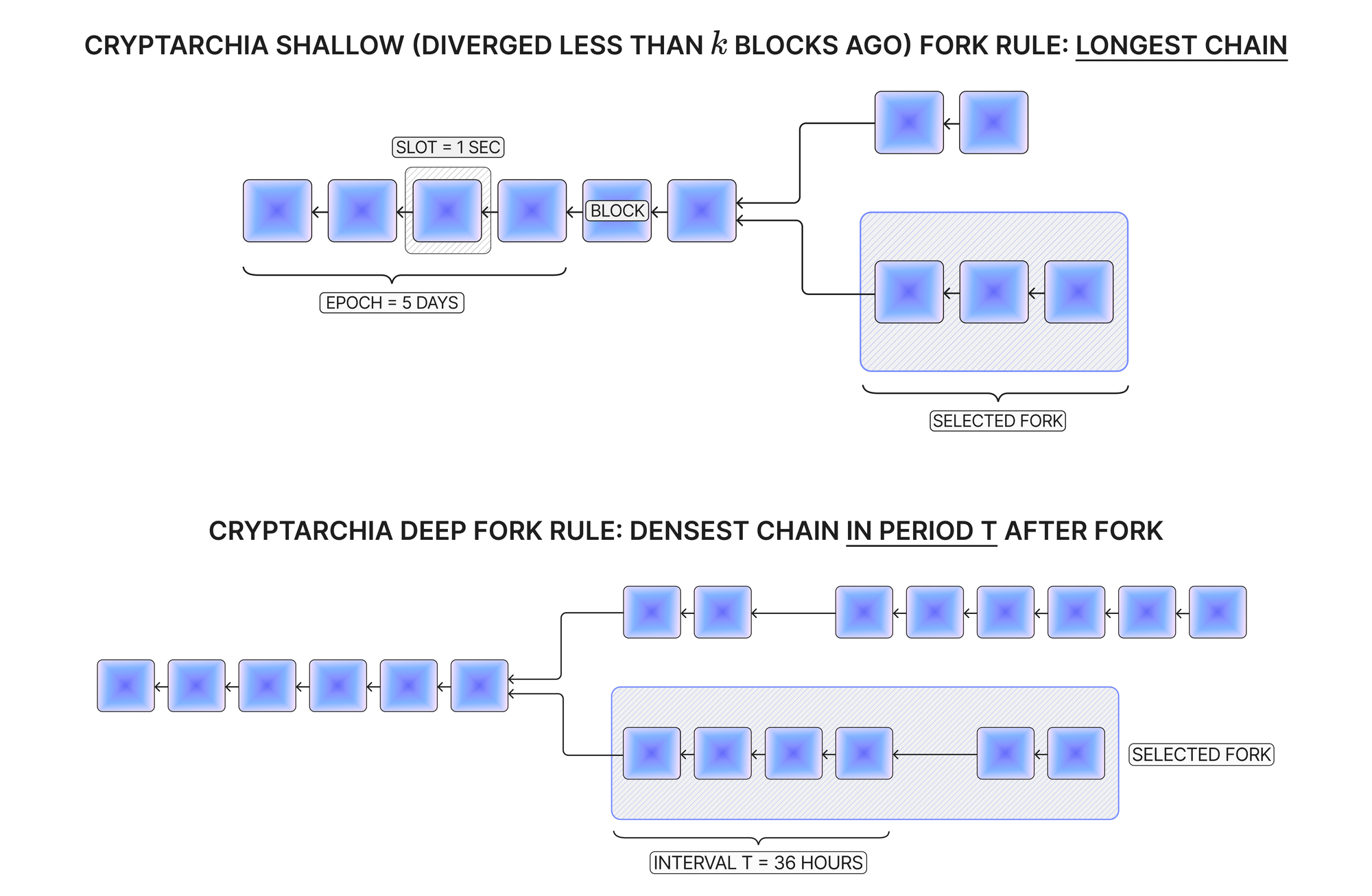
Generally speaking, Cryptarchia is very similar to its predecessor, Crypsinous. Following the Ouroboros model, Cryptarchia divides time into basic units called slots that are grouped into larger units called epochs. Each slot allows for the addition of at most one block to a given chain, while each new epoch refreshes the leadership election parameters and eligibility set. The fork choice rule, inherited from Ouroboros Genesis, involves selecting the longest chain for shallow forks and the densest chain for deep forks to ensure that honest parties can join or rejoin the protocol without trust assumptions. The above model is described in the following diagram.

Figure 1. Cryptarchia’s fork choice rule and time divisions.

Cryptarchia notes, the equivalents of coins in Crypsinous, each have their own secret key for spending, and a corresponding public key for receiving new notes. Transfer transactions are implemented according to the UTXO model, where notes belonging to the sender are spent and new notes belonging to the recipient are created with the same total value. Transaction information is hidden, with its validity verified using zero knowledge proofs.

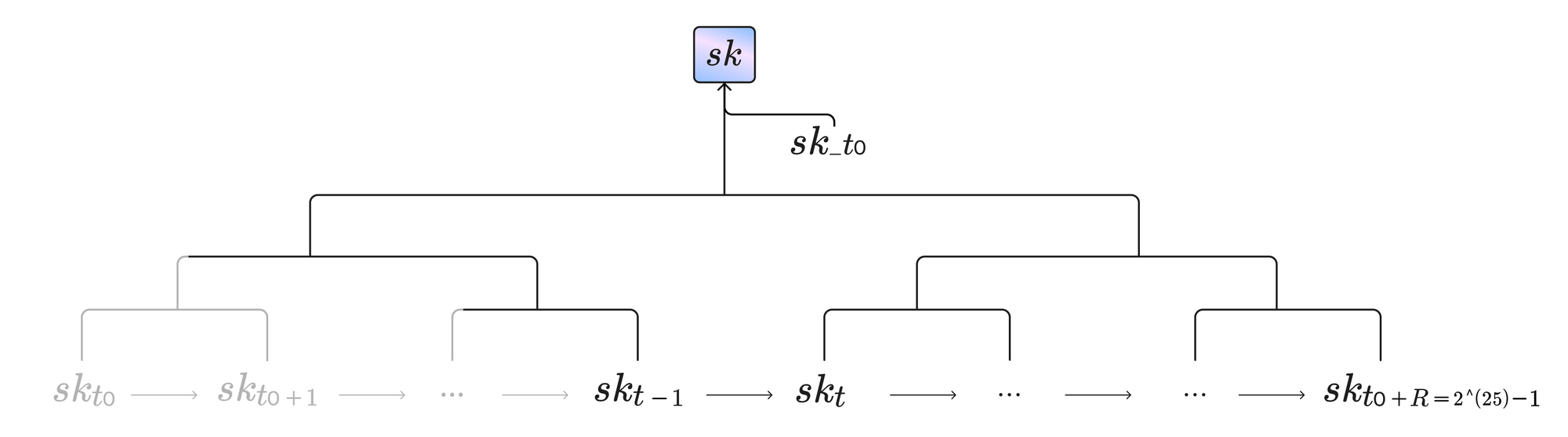
Each slot presents an opportunity for a block leader to add a block to the chain. The leadership election is run locally for each individual eligible note using information obtained from the previous epoch. The owner of a note that won an election can propose a new block, which will contain a Proof of Leadership (PoL). Most slots will have no valid leader to allow parties to synchronise, while some will have one or even several leaders. To ensure that an adaptive adversary who corrupts an honest participant will not be able to generate Proofs of Leadership for past slots, Nomos notes use a key deletion protocol. A note’s secret key, shown in the diagram below, is taken from the root of a Merkle tree consisting of $2^{25}$ leaves hashed together with its first slot. Each leaf in the tree corresponds to a slot, and is deterministically derived from the previous slot to use less storage space. Once a slot passes, the corresponding leaf is deleted.

Figure 2. The secret key tree in Cryptarchia, illustrating its key deletion functionality.

Changes Introduced in Cryptarchia

Notes

In place of Crypsinous coins, Cryptarchia uses notes to represent data more generally, with these data being private by default. Notes are bound to their owners and have a common framework to enable them to be transferred between Nomos zones, the autonomous network state rollapps that form the client-facing part of the Nomos Network. As mentioned above, note transfer transactions are based on the UTXO model where a sender spends their note and creates an equivalent note belonging to the recipient.

The expanded variety of use cases for notes as compared to coins, as well as the more complex nature of zone ledgers (see below), has required each note to contain more private data fields. These data, known only to the creator and owner of the note, include:

$state$: The private data attached to the note. The note state can contain any type of information, with no requirement for a specific interpretation or structure.
$v$: The value associated with the note. For an asset note, $v$ represents the note’s asset value.
$U$: The unit tied to the value. This can be understood as the “type” of the note.
$nonce$: An arbitrary value to ensure the uniqueness of each note.
$ZoneID$: The identifier of the zone where the note resides.

The unit field will determine the specific rules, known as covenants, that govern spending notes and creating or destroying note value. The unit will also determine whether the note can participate in consensus.

Zone Ledgers

Crypsinous maintains a protocol-wide Merkle tree of commitments to coins eligible for spending and another for those eligible for leadership, as well as a set of serial numbers representing spent coins. These commitment trees and serial number set are used to ensure that transactions use eligible coins and avoid double-spending, all while ensuring that the coin data remain private. By contrast, Nomos’ modular architecture gives each zone its own ledger, relying on the Bedrock to enforce correctness and interoperability. Each Nomos zone maintains just two Merkle trees: one for commitments of notes eligible for spending, and another of nullifiers representing spent notes.

A zone’s commitment set contains commitments to every note created in that zone. The commitment to a note is calculated by taking the hash of its concatenated private data (see above) appended to the note’s public key, creating a binding identifier for the note without revealing its data. The commitment set is organised as a Merkle Mountain Range (MMR) tree, which arranges the data into a set of the largest possible full binary Merkle trees, whose roots are then hashed together to create the MMR tree’s root. Zone executors only need to store the roots of these subtrees, known as frontier nodes, in their commitment set, resulting in a “compressed” set that does not balloon in size as the amount of zone notes grows. A visual example of an MMR is shown below.

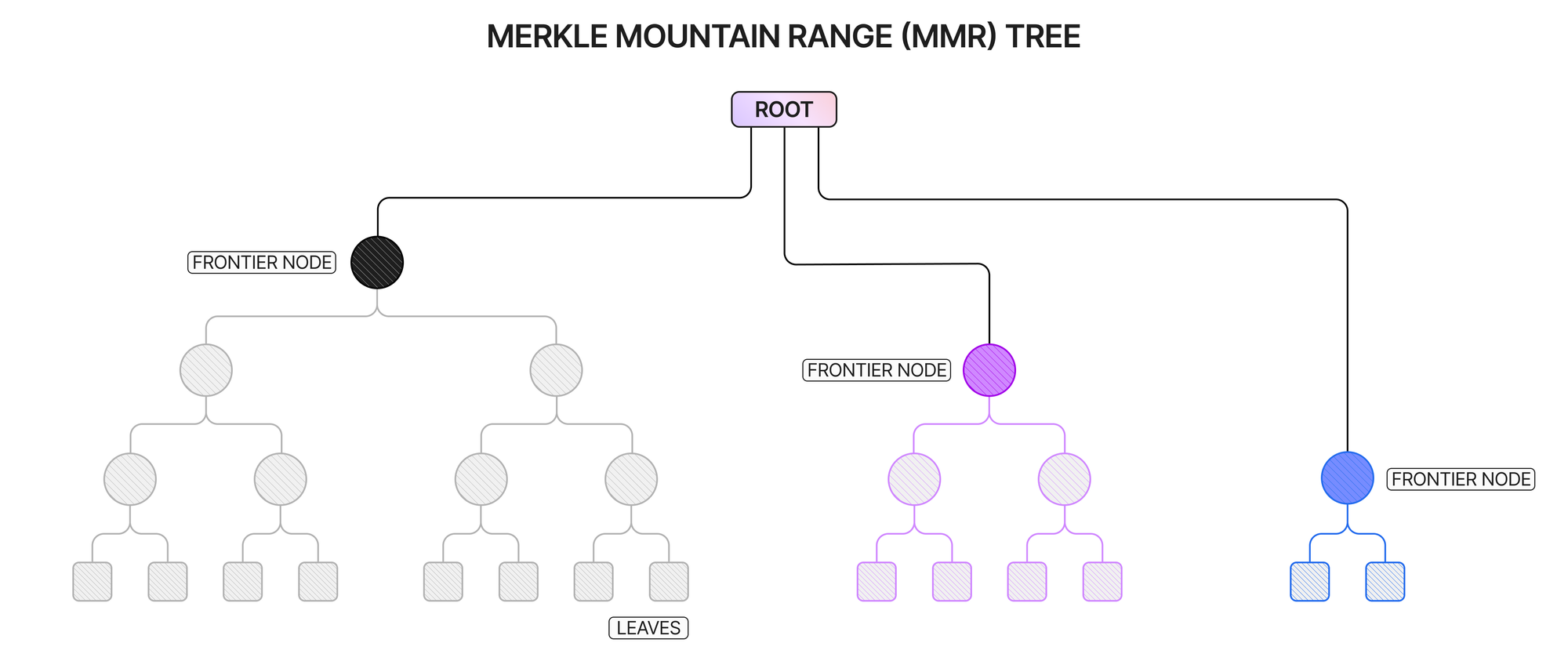
Figure 3. A Merkle Mountain Range (MMR) tree.

Proving that a note exists in a zone requires a Merkle proof of membership in the commitment set.

Meanwhile, a zone’s nullifier set stores nullifiers that represent notes spent in the zone. Like a serial number in Crypsinous, a note nullifier’s absence in a zone’s nullifier set means that the note has not yet been spent. However, the nullifier is calculated as the hash of the note’s secret key appended to its commitment, rather than of just its secret key and nonce as in Crypsinous. In addition, a proof of non-membership in the nullifier set must be produced for a note in order to spend it. This is in contrast to Crypsinous’ method of simply revealing the serial number and having validators verify its non-membership in the set of serial numbers.

The nullifiers in a nullifier set are organised as an Indexed Merkle tree (IMT). This type of Merkle tree inserts leaves in a sorted way, with each leaf also including a pointer to the next-highest value leaf. Due to the presence of these pointers, IMTs are especially convenient for computing proofs of non-membership.

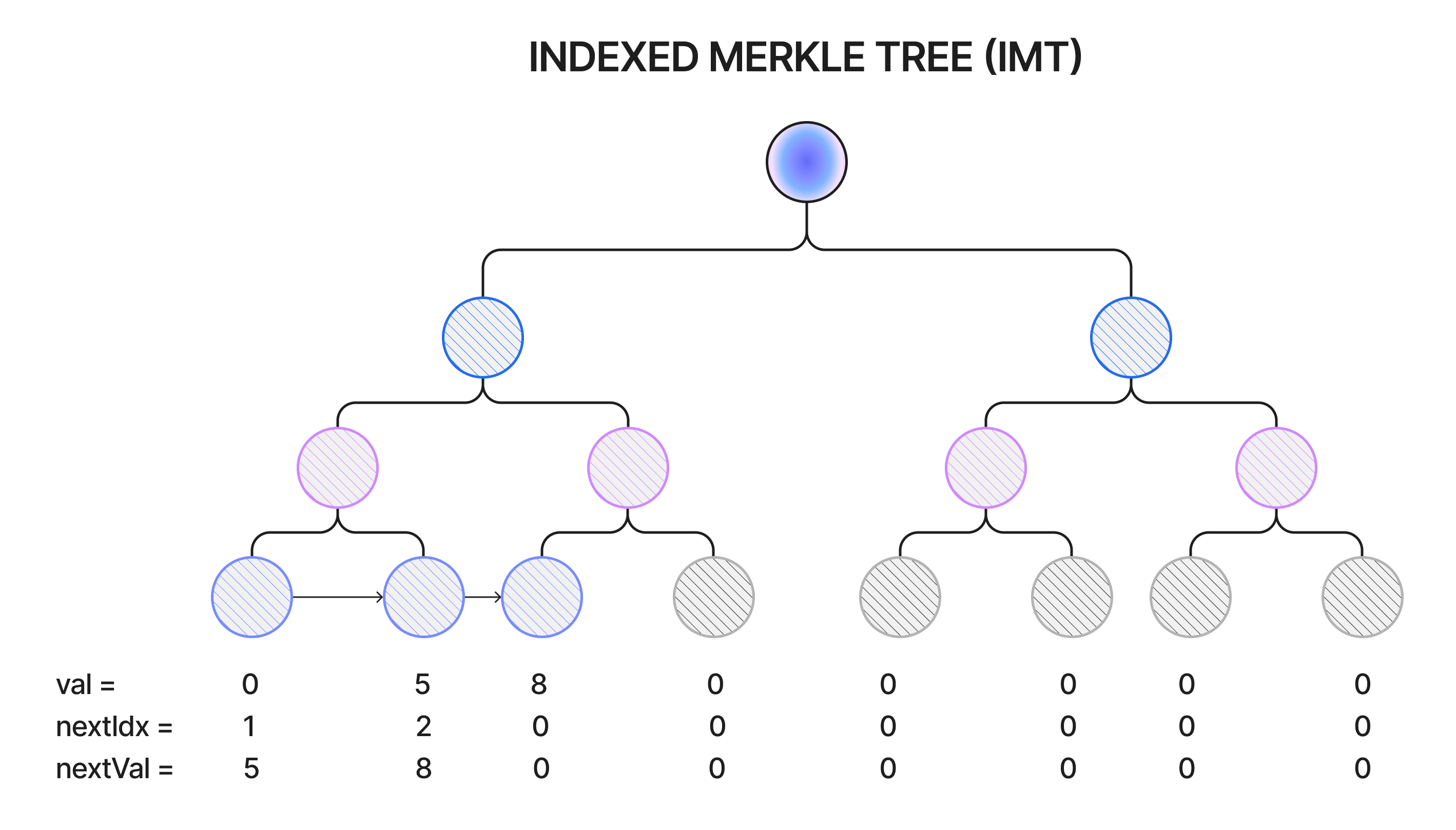
It is important to note that making users responsible for providing proofs of nullifier non-membership renders the Crypsinous coin evolution tactic not necessary in Cryptarchia. This is because a nullifier non-membership proof does not reveal any information about the note itself and does not affect that coin’s eligibility for spending.

Estimating Total Stake

The leadership election in Crypsinous compares the output of a pseudorandom function to a threshold value $T_c$ that depends on the stake of a coin $c$ relative to the total stake - that is, the total coin value eligible for leadership in a given epoch. If the output is less than $T_c$, the coin $c$ is selected for leadership. Due to the privacy properties of Crypsinous, calculating the total active stake cannot be done directly, making it far from straightforward to obtain the relative stake for a given coin. Despite this, the authors of the Crypsinous paper did not include a method for estimate relative stake, leaving this problem to be solved in implementation.

To implement Cryptarchia, the Nomos team was tasked with designing a way to estimate the total stake. This estimate is based on the fact that the rate of block production, which is correlated with the total stake, can be calculated by any participant. Based on simulations, the Nomos team derived the following formula to be used for estimating total stake $D^{ep+1}$ in the epoch number $ep+1$:

$$ D^{ep+1}=D^{ep}-\beta\frac{D^{ep}}{\log\left(\frac{1}{1-f}\right)}\left(\log\left(\frac{1}{1-f}\right)-\frac{N}{T}\right) $$

$\frac{N}{T}$ is the observed number of valid blocks $N$ proposed during the inference period $T$ of epoch $ep$. $T$ is defined as the first three fifths of slots in $ep$, or around 3 days. Because there can be more than one valid block leader for a given slot, blocks added to discarded forks in that slot are also counted. This observed rate is to be contrasted with the target rate $\log\left(\frac{1}{1-f}\right)$ - the “ideal” rate of blocks per slot in the scenario where all participants have the same stake. The target rate is calculated based on the slot activation coefficient $f=0.05$ - the target rate of blocks per slot in the scenario where the entire stake is controlled by one party.

To obtain a correction value for the total stake estimate, the observed rate is subtracted from the target rate. To avoid instability and drastic changes to the leadership election, the correction value is multiplied by a “learning rate” that controls how quickly the estimate responds to observed changes. The learning rate is obtained by dividing the previous epoch’s total stake estimate $D^{ep}$ by the target rate $\log\left(\frac{1}{1-f}\right)$ and multiplying that by the learning rate coefficient $\beta=0.8$. The chart below shows how the total stake estimation formula above reaches equilibrium 2 epochs after a drastic 50% reduction in active stake.

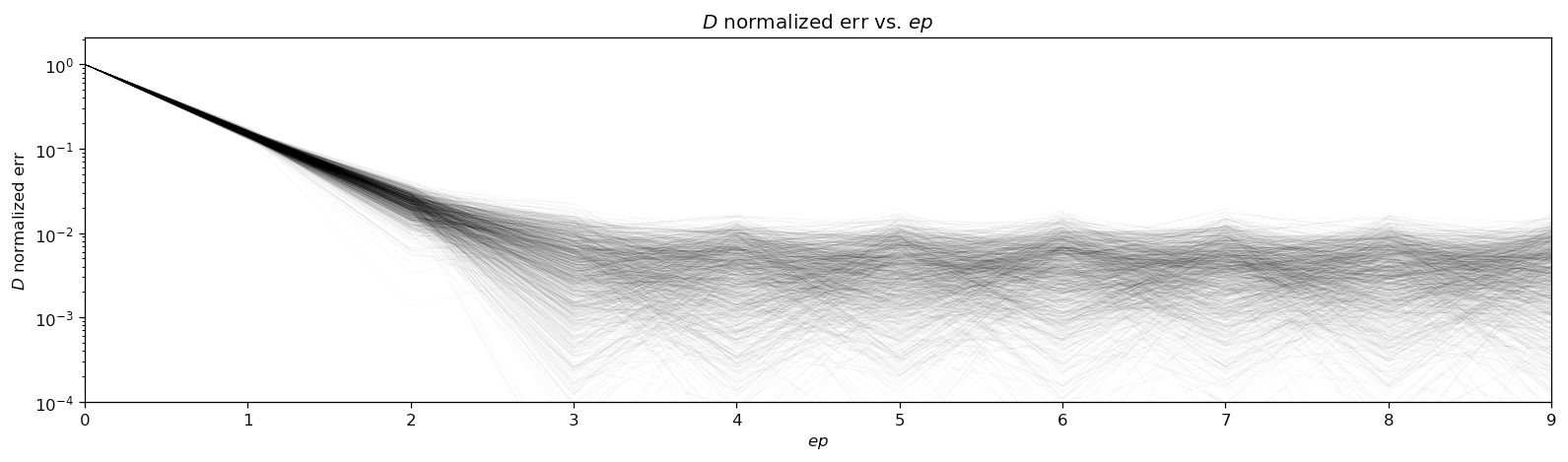
Figure 5. Simulation results for the total stake estimate D after a 50% reduction of the active stake at epoch 0.

Finally, the resulting correction value is subtracted from the previous epoch’s stake estimate to yield the estimate for the current epoch $ep+1$. Calculating relative stake is as simple as dividing a note’s value $v$ by the total stake estimate $D^{ep+1}$.

Wealth Concentration Concerns with Crypsinous

It is important to note that some researchers have expressed concern over the possibility of Ouroboros Crypsinous displaying a tendency of wealth concentration toward a minority of participants. Due to this concern, L1 blockchain DarkFi notably chose to move away from using Crypsinous for consensus in favour of PoW mining algorithm RandomX. However, the Nomos team has discovered that this tendency toward wealth concentration is not present in Cryptarchia when relying on the formula above for estimating total stake. More detailed information on this result, as well as an analysis of the effect of various fork choice rules on wealth concentration, can be found in the following articles:

Leadership Election

To be eligible for block leadership in a given epoch, a note must have been in existence since at least the beginning of the previous epoch. To keep track of notes of sufficient age, validators maintain a set of commitments to notes eligible for leadership based on a snapshot taken at the beginning of each epoch. Whether a particular note wins the leadership election for a given slot is determined by comparing some hashed data (the ticket) to a threshold derived from the note’s relative stake. The lottery ticket is calculated by hashing the concatenated value of:

The constant “LEAD”,
The epoch nonce $\eta_{ep}$,
The slot number $sl$,
The note commitment $cm$,
And its secret key $sk$.

$\eta_{ep}$ is updated each epoch based on an evolving tentative nonce calculated in every block, with added randomness contributed by block leaders. A block’s tentative epoch nonce $\eta'$ is set to be the hash of the concatenation of:

The constant “EPOCH_NONCE”,
The tentative nonce $\eta'_{parent}$ of the previous block regardless of the epoch it is in,
The randomness contribution $\rho_{sl}$ for a block in that slot,
And the slot number $sl$.

$\rho_{sl}$ is calculated by taking the hash of the slot number and nullifier of the winning note.

For the purposes of calculating the epoch nonce, an epoch $ep$ is divided into three periods. At the beginning of the stake distribution snapshot period, which corresponds to the first 30% of slots in $ep$, a snapshot is taken of all notes that can participate in consensus. The snapshot, which is finalised by the end of this period, will be used as the set of eligible notes for the leadership election in the following epoch $ep+1$. The buffer period corresponding to the second 30% of slots in $ep$ is used as a waiting phase to ensure that at least one honest participant wins a leadership election and contributes to the randomness of the epoch nonce as described above. The tentative nonce at the end of the buffer period becomes the epoch nonce for the following epoch. Finally, the epoch nonce for the following epoch $\eta_{ep+1}$ is revealed at the beginning of the lottery constants finalisation period, which takes up the remaining two fifths of the epoch. Cryptarchia’s epoch schedule is shown in the diagram below.

Figure 6. Cryptarchia’s epoch schedule, with an example blockchain demonstrating how the epoch nonce is calculated.

The threshold that the ticket is compared to is calculated using a function that depends on the note’s relative stake, similar to Crypsinous. To make the zero knowledge proof more efficient to calculate, Cryptarchia approximates Crypsinous’ threshold function using a Taylor expansion of order 2. If the ticket is less than the threshold, the note has won the leadership election and its owner can produce a block with an associated Proof of Leadership (PoL).

The zero knowledge Proof of Leadership submitted with a new block proves that:

The note’s nullifier, commitment, and secret key were calculated correctly
The note’s commitment is in the set of aged notes
The note’s nullifier is not in the nullifier set
The ticket and threshold are calculated correctly
The ticket is less than the threshold
The leader knows the secret key leaf corresponding to the block’s slot
The randomness contribution is calculated correctly

Sources and Further Reading